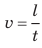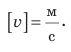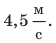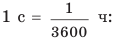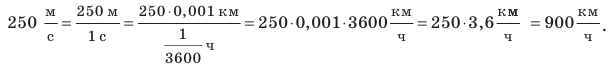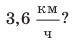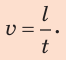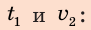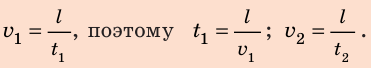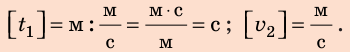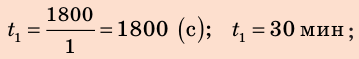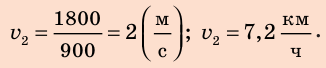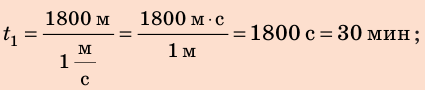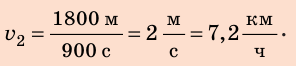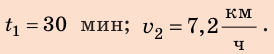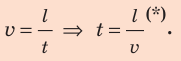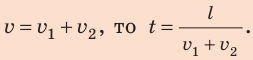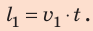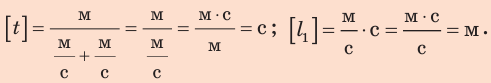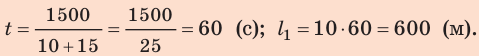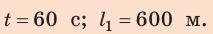Что такое скорость прямолинейного равномерного движения физическая величина равная

Содержание:

Равномерное движение:

В репортажах с автомобильных гонок, сообщениях о погоде можно, например, услышать: «Скорость движения автомобиля-победителя перед финишем достигла 250 километров в час»; «Скорость ветра достигала 25 метров в секунду» и т. п. Что это значит? Как сравнить эти скорости?

Слово «скорость» вы знаете давно. Поэтому, когда слышите, что скорость движения автомобиля составляет 20 метров в секунду, то понимаете: автомобиль, двигаясь с такой скоростью, каждую секунду проходит расстояние 20 м.

Подумайте, какое расстояние проедет этот автомобиль за 10 секунд; за полсекунды; за 0,1 секунды. Скорее всего, большинство из вас ответили так: за 10 с автомобиль проедет 200 м, за полсекунды — 10 м, за 0,1 с — 2 м. И эти ответы правильны, если считать, что за любые (малые или большие) равные интервалы времени автомобиль проезжает одинаковый путь. То есть если автомобиль движется равномерно.

Равномерное движение — это механическое движение, при котором тело за любые равные интервалы времени проходит одинаковый путь. Обратите внимание на слова «любые равные интервалы времени». Иногда, рассматривая даже неравномерное движение тела, можно выделить такие равные интервалы времени, за которые тело проходит одинаковые расстояния. Например, каждые 30 с пловец проплывает дорожку в бассейне (25 м), но нельзя утверждать, что он движется равномерно, ведь при развороте он замедляет движение.

Равномерное прямолинейное движение

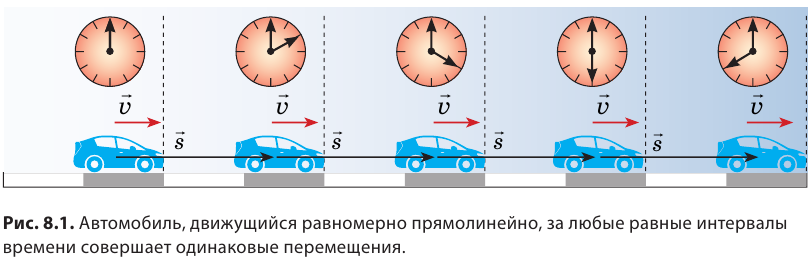
Если автомобиль равномерно движется по прямолинейному участку дороги, то за равные интервалы времени он совершает одинаковые перемещения (рис. 8.1), то есть проходит одинаковый путь и не изменяет направления своего движения. Такое движение называют равномерным прямолинейным.

Равномерное прямолинейное движение — это механическое движение, при котором за любые равные интервалы времени тело совершает одинаковые перемещения. Равномерное прямолинейное движение — простейший вид движения, который в жизни встречается редко. Примерами такого движения могут быть движение автомобиля на прямолинейном участке дороги (без разгона и торможения), падение металлического шарика в растительном масле, полет парашютиста через некоторое время после раскрытия парашюта.

Определение скорости равномерного движения

Полагаем, вам несложно определить скорость равномерного движения, например, пешехода, который прошел 30 м за 20 с. Из курса математики вы хорошо знаете, что для этого нужно путь, который прошел пешеход (l = 30м), разделить на время его движения (t = 20c).

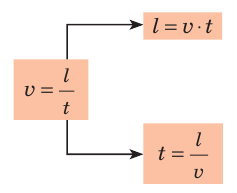
Скорость равномерного движения (v) — это физическая величина, равная отношению пути l, пройденного телом, к интервалу времени t, в течение которого этот путь был пройден:

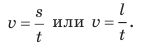
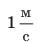
Обратите внимание! В ходе равномерного прямолинейного движения модуль перемещения равен пути ( s= )l, поэтому значение скорости движения можно определить по любой из формул: В Международной системе единиц путь измеряют в метрах, время — в секундах, поэтому единица скорости движения в СИ — метр в секунду: равен скорости такого равномерного движения, при котором тело за 1 с проходит путь 1 м. Прибором для прямого измерения скорости движения служит спидометр.

Скорость движения

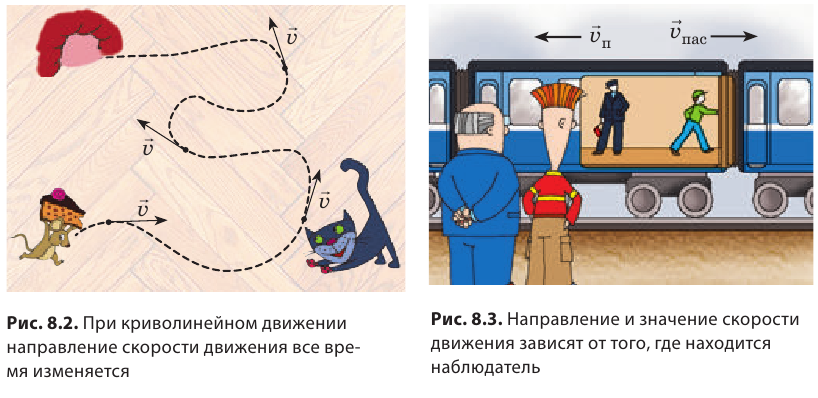
Скорость движения — векторная величина: она имеет не только значение, но и направление. На рисунках направление скорости движения тела показывают стрелкой (см. рис. 8.1, 8.2).

Если тело движется равномерно прямолинейно, то значение и направление скорости движения остаются неизменными (см. рис. 8.1). Если тело движется равномерно по криволинейной траектории, значение скорости движения остается неизменным, а направление все время изменяется (рис. 8.2). Направление и значение скорости движения зависят от того, относительно какого тела рассматривают движение. Представьте, что вы стоите в вагоне поезда, движущегося на восток (рис. 8.3). Поезд проезжает мимо станции со скоростью 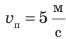. 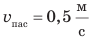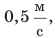В это время другой пассажир идет по вагону со скоростью , двигаясь в направлении, противоположном движению поезда. Как вы считаете, одинаковой ли будет скорость движения пассажира для вас и для людей, стоящих на перроне? Конечно, нет! Для вас пассажир движется на запад со скоростью а для людей на перроне он вместе с поездом движется на восток со скоростью

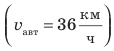
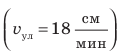
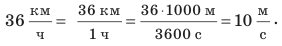
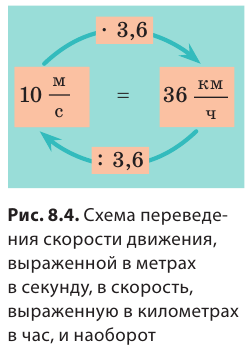
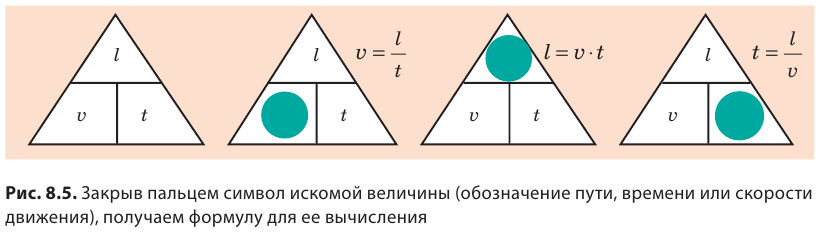
Значение скорости движения может быть выражено не только в метрах в секунду, но и в других единицах. Например, автомобиль движется со скоростью 36 километров в час , ракета мчится со скоростью 8 километров в секунду , улитка ползет со скоростью 18 сантиметров в минуту Для решения задач нужно научиться представлять скорость движения, данную в одних единицах, в других единицах. Например, скорость движения автомобиля — 36 км/ч. Чтобы представить эту скорость в метрах в секунду, вспомним, что 1 ч = 3600 с, а 1 км = 1000 м. Тогда: Попробуйте представить в метрах в секунду скорости движения ракеты и улитки (приведены выше). Сложнее переводить в другие единицы скорость движения, данную в метрах в секунду, но последовательность действий остается той же. Например, скорость движения самолета — 250 м/с. Представим ее в километрах в час, вспомнив, что 1 м = 0,001 км;

Чтобы скорость движения, представленную в метрах в секунду, выразить в километрах в час (и наоборот), можно воспользоваться схемой, приведенной на рис. 8.4.

Определяем путь и время движения тела

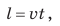
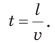
Из курса математики вы знаете: если известны скорость и время движения тела, то можно найти путь, который прошло тело. Для этого нужно скорость движения умножить на время: где l — путь; v — скорость движения; t — время движения с данной скоростью. Если известны путь и скорость движения тела, можно найти время движения тела. Для этого необходимо путь разделить на скорость движения: Иногда для определения пути, скорости или времени движения тела удобно пользоваться «волшебным треугольником» (рис. 8.5).

Итоги:

Равномерное движение — это механическое движение, при котором за любые равные интервалы времени тело проходит одинаковый путь. Равномерное прямолинейное движение — это механическое движение, при котором за любые равные интервалы времени тело совершает одинаковые перемещения. Скорость равномерного движения — это физическая величина, равная отношению пути, который прошло тело, к интервалу времени, в течение которого этот путь был пройден: 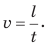Единица скорости движения в СИ — метр в секунду (м/с). Спидометр — прибор для прямого измерения скорости движения тела. Кроме значения скорость движения имеет направление. Направление и значение скорости движения тела зависят от выбора системы отсчета.

Может, вы будете удивлены, но в повседневной жизни вы уже встречались с физическими задачами и даже решали их. Приведем несколько примеров физических задач, прокомментируем основные этапы их решения, и в дальнейшем вы будете подходить к решению таких задач как настоящие физики.

Пример №1

Предположим, что до начала уроков остается 15 минут, а вы знаете, что расстояние от вашего дома до школы равно 1800 м. Придете ли вы вовремя, если будете идти со скоростью

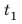
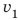
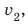
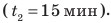
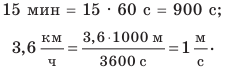
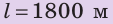
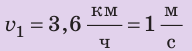
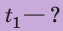
С какой наименьшей скоростью вы должны идти, чтобы не опоздать? Анализ физической проблемы. В задаче нужно найти: 1) время движения до школы с указанной скоростью ; 2) наименьшую скорость с которой следует идти, чтобы затратить на путь не более 15 мин Движение будем считать равномерным. Скорость движения дана в , а путь — в единицах СИ. Представим время и значение скорости движения в единицах СИ: Закончив анализ, запишем краткое условие задачи.

, , .

,.

Решение:

Движение равномерное, поэтому воспользуемся формулой для расчета скорости равномерного движения:

Найдем выражения для расчета искомых величин

Проверим единицы искомых величин:

Найдем числовые значения искомых величин:

Обратите внимание! Для получения ответа в выражение для искомой величины можно сразу подставлять и числовые значения, и единицы известных величин. В этом случае запись будет такой:

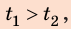
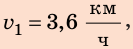
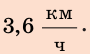
Анализ результатов. Поскольку то, двигаясь со скоростью вы не успеете к началу уроков. Чтобы не опоздать, нужно двигаться со скоростью, значение которой больше Именно такое значение получено в ходе решения. Следовательно, полученные значения искомых величин вполне правдоподобны.

Ответ:

Пример №2

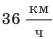
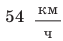
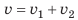
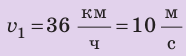
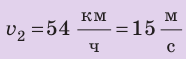
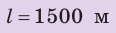
По озеру навстречу друг другу равномерно прямолинейно движутся два катера. На начало наблюдения расстояние между катерами составляло 1500 м. Скорость движения первого катера равна , второго — . Через какое время катера встретятся? Какое расстояние пройдет до встречи первый катер? Анализ физической проблемы. Катера движутся навстречу друг другу. Это значит, что они приближаются друг к другу со скоростью с этой же скоростью проходят расстояние l =1500 м. Задачу будем решать в единицах СИ.

,,.

,.

Решение:

По определению скорости движения:

Так как

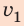
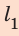
Зная время t и скорость движения , определим путь , который пройдет первый катер до встречи:

Проверим единицы искомых величин:

Определим числовые значения искомых величин:

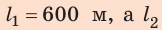
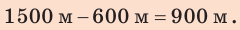
Анализ результатов. Так как первый катер движется медленнее второго, то до момента встречи он пройдет меньший путь. Такой результат и получен: соответственно Поэтому результаты вполне реальны.

Ответ:

Графики равномерного движения

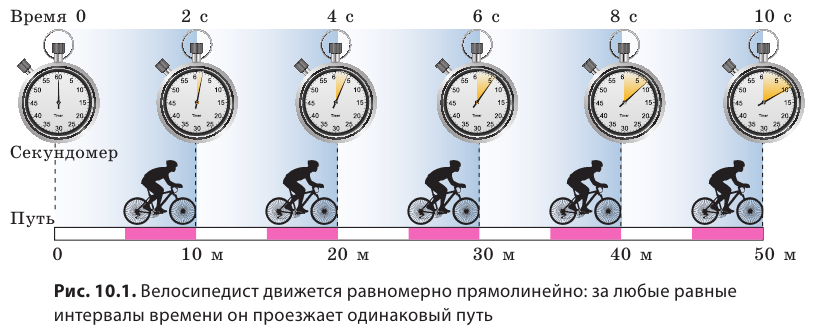
Велосипедист едет по трассе (рис. 10.1). Скорость движения, которую показывает спидометр велосипеда в любой момент времени, равна 5 м/с. Как описать движение велосипедиста и вообще любого тела с помощью графиков? Вспомним, ведь графики движения тел вы изучали в курсе математики 6 класса.

График зависимости пути от времени для равномерного движения тела

Построим график зависимости пути, который проезжает велосипедист (см. рис. 10.1), от времени наблюдения — график пути. Для построения графика выполним следующие действия.

Рассуждая аналогично, получим:

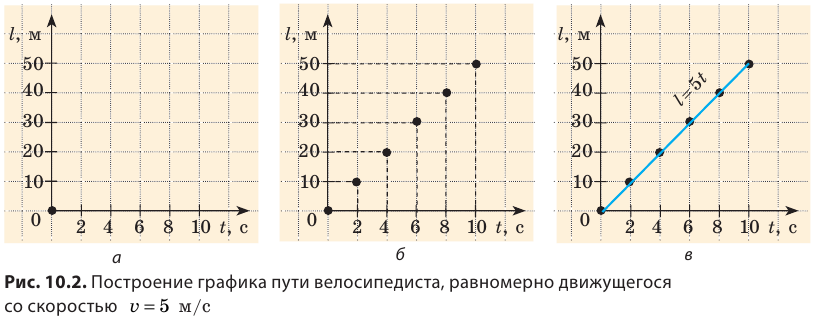
2. Проведем две взаимно перпендикулярных оси. На горизонтальной оси — оси абсцисс — отложим время движения велосипедиста в секундах (t, с) так, что одной клетке будет соответствовать интервал времени 2 с. На вертикальной оси — оси ординат — отложим путь в метрах (l, м) так, что одной клетке будет соответствовать путь, равный 10 м (рис. 10.2, а).

3. Построим точки с координатами: (0; 0), (2; 10), (4; 20), (6; 30), (8; 40), (10; 50). Абсциссы данных точек соответствуют времени движения спортсмена, ординаты соответствуют пути, который он проехал за это время (рис. 10.2, б).

4. Соединим построенные точки линией (рис. 10.2, в). Полученный отрезок прямой — график пути велосипедиста.

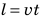
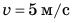
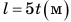
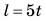
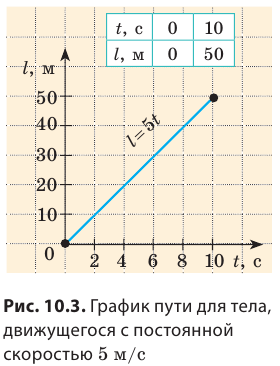
Обратите внимание! Велосипедист движется равномерно, поэтому путь, который он проезжает, можно определить по формуле , в любой момент времени ; поэтому можно записать: , где время t дано в секундах. Равенство — уравнение зависимости пути, который проезжает велосипедист, от времени наблюдения.

При равномерном движении график пути — это всегда отрезок прямой, наклоненной под определенным углом к оси времени. Поэтому для построения графика пути достаточно определить путь l для двух значений времени t и через полученные две точки провести отрезок прямой. Например, чтобы построить график пути велосипедиста, можно взять время начала наблюдения t(=0 )и время окончания наблюдения ( t = 10 с) (рис. 10.3).

Что можно узнать по графику пути

График пути дает много полезной информации.

По графику пути можно:

Пример №3

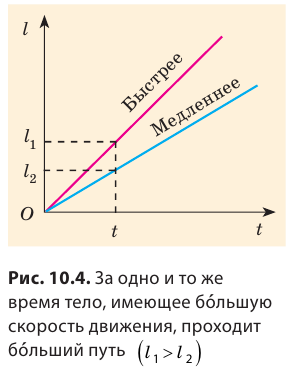
По графику пути, представленному на рис. 10.5, узнайте: 1) как двигалось тело; 2)какой путь прошло тело за первый час; за следующие два часа; 3) какой была скорость движения тела на каждом участке.

Решение:

По графику видим, что весь путь состоит из трех участков, на каждом из которых тело двигалось равномерно (график пути тела — отрезки прямых). Участок I. По графику видим, что путь, пройденный телом за первый час, равен 20 км, поэтому скорость движения тела составляла: Участок ІI. За следующие два часа тело прошло путь . Соответственно скорость движения тела была равна:

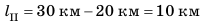
Участок ІІI. Последний час путь не изменялся, значит, тело остановилось: 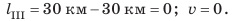Анализ результатов. По графику видим, что участок I графика образует с осью времени больший угол, чем участок IІ. Поэтому участок І соответствует большей скорости движения тела.

Строим график скорости равномерного движения тела

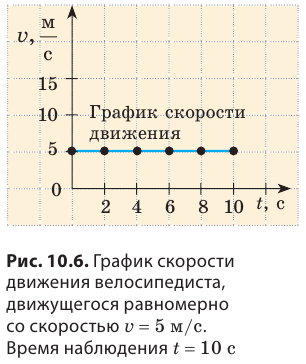
Вернемся к велосипедисту, движущемуся равномерно со скоростью v = 5 м/с (см. рис. 10.1). Построим график зависимости скорости его движения от времени наблюдения — график скорости движения. Для построения графика выполним следующие действия.

1. Заполним таблицу соответствующих моментов времени t движения велосипедиста и скорости движения v, которую он имел в эти моменты времени:

Велосипедист двигался равномерно, поэтому скорость его движения оставалась неизменной в течение всего времени наблюдения.

2. Проведем две взаимно перпендикулярных оси. На оси абсцисс отложим время движения велосипедиста в секундах (t, с), на оси ординат — скорость движения в метрах в секунду 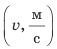(рис. 10.6).

3. Построим точки с координатами (0; 5), (2; 5), (4; 5), (6; 5), (8; 5), (10; 5). Абсциссы указанных точек соответствуют времени движения спортсмена, ординаты — скорости его движения.

4. Соединим точки линией. Полученный отрезок прямой — график скорости движения велосипедиста. При равномерном движении график скорости движения тела — отрезок прямой, параллельной оси времени.

Что можно узнать по графику скорости движения тела

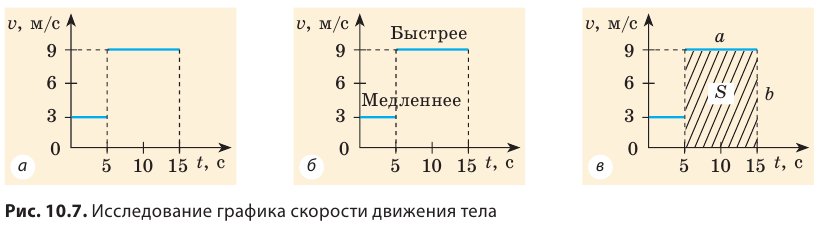
Рассмотрим график скорости движения некоторого тела (рис. 10.7, а) и узнаем о движении данного тела как можно больше.

1. В течение интервалов времени от 0 до 5 с и от 5 до 15 с тело двигалось равномерно, поскольку соответствующие участки графика скорости его движения — отрезки прямых, параллельных оси времени.

2. Скорость движения тела в течение последних 10 с наблюдения больше, чем в течение первых 5 с, поскольку второй участок графика расположен дальше от оси времени, чем первый участок (рис. 10.7, б).

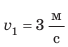
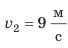
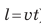
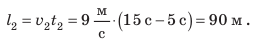
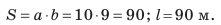
В данном случае: — на интервале времени от 0 до 5 с; — на интервале времени от 5 до 15 с. 3. Можно определить путь l, который прошло тело (вспомните: ). Так, за интервал времени от 5 до 15 с тело прошло путь 90 м: Этот путь численно равен площади заштрихованного прямоугольника (рис. 10.7, в): Обратите внимание! Для любого движения числовое значение пути, который прошло тело, равно числовому значению площади фигуры под графиком скорости движения этого тела.

Итоги:

При равномерном движении тела график пути — это всегда отрезок прямой, наклоненной под определенным углом к оси времени, а график скорости движения — это отрезок прямой, параллельной оси времени.

По графику пути можно:

По графику скорости движения можно:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник