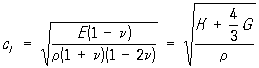Что такое скорость звука в воздухе
Скорость звука и число М
Для начала давайте выясним, сверхзвук — это сколько км/ч? Какова должна быть скорость, чтобы считаться сверхзвуковой? Проблема в том, что простого и однозначного ответа на этот вопрос… Просто нет.
Есть правильный ответ — больше 1 М. Или Число Маха равное единице, это скорость звука, а выше единицы, это уже сверхзвук.
Совсем не привычное нам число, выраженное в километрах в час. Если упростить, то объяснить можно так: скорость звука зависит о свойств среды в которой он распространяется, чем плотнее среда, тем быстрее распространяются колебания (звук это ведь волна). Таким образом на разной высоте скорость звука разная. Чем выше, тем меньше плотность воздуха и тем ниже будет местная скорость звука.
Что такое скорость звука
Скорость звука в километрах в час не выражается, просто потому, что в таком случае она всегда будет разной.
Зависимость скорости звука от высоты полета
Например, скорость звука у земли (на высоте 0 км) составит 340 метров в секунду (м/с), это 1224 км/ч. И тут важно сказать что такое значение будет: при температуре +15 и давлении 750 мм. рт. ст. и относительной влажности 0%. То есть, при «стандартных» условиях.
А вот на высоте 10 000 метров, на которой летают современные пассажирские лайнеры, это уже около 299 м/с (это 1076 км/ч), то есть разница довольно значительная — 12%.
Также от высоты полета и других параметров атмосферы зависит и скорость звука, и сопротивление воздуха и, соответственно, скорость самолета, которую он может развить.
Скорость звука на высоте 11 километров и выше почти не будет меняться, эта часть атмосферы называется «тропопауза».
То же самое в виде таблицы
Зависимость скорости звука от высоты*
| Высота, м | Скорость звука, м/с | Скорость звука, км/ч |
| -1000 | 344,1 | 1 238,8 |
| 0 | 340,3 | 1 225,1 |
| 1000 | 336,4 | 1 211,0 |
| 2000 | 332,5 | 1 197,0 |
| 3000 | 328,6 | 1 183,0 |
| 4000 | 324,6 | 1 168,6 |
| 5000 | 320,6 | 1 154,2 |
| 6000 | 316,5 | 1 139,4 |
| 7000 | 312,3 | 1 124,3 |
| 8000 | 308,1 | 1 109,2 |
| 9000 | 303,9 | 1 094,0 |
| 10000 | 299,6 | 1 078,6 |
| 11000 | 295,2 | 1 062,7 |
| 12000 | 295,1 | 1 062,4 |
| 13000 | 295,1 | 1 062,4 |
| 14000 | 295,1 | 1 062,4 |
*Минутка занудства. Нужно напомнить, что на самом деле скорости звука от высоты зависит условно, это упрощение. Скорость звука зависит от плотности атмосферы, а плотность воздуха, в свою очередь, зависит от температуры, влажности и давления, которые меняются с высотой.
Зачем нужно число Маха
Так вот, число Маха в авиации представляет собой отношение скорости летательного аппарата к скорости звука на той высоте на которой он сейчас летит. Так удобнее, ведь на разной высоте скорость звука будет разной и чтобы понимать достигает ли самолет скорости звука, его скорость измеряют в числах М.
Один мах, это просто — 1 мах, а не «км/ч». Нельзя просто ответить на вопрос «сколько 1 мах в километрах в час», нужно всегда уточнять, о какой высоте идет речь.
Если еще проще, число М показывает сколько скоростей звука в скорости самолета сейчас на конкретной высоте (при определенных условиях среды). Если число Маха больше единицы, очевидно, мы имеем дело со сверхзвуковой скоростью. Поэтому чаще всего вы будете встречать пояснение для какой высоты указано конкретное число Маха.
Например, для Боинга 777 крейсерской скоростью считается 0,84 М (это дозвуковой летательный аппарат). То есть на высоте 10 000 метров при стандартных условиях, принимая скорость звука за 1076 км/ч умножаем ее на 0,84 и получаем — 904 км/ч. По документации крейсерская скорость Boeing 777 составляет как раз 905 км/ч.
Что касается сверхзвуковых летательных аппаратов, то, по определению, их скорости должны быть больше скорости звука, то есть больше 1 М. Например у Су-27 это 2,35 М, что примерно 2 528 км/ч на высоте 10 км (скорость звука 295 м/с, а это 1062 км/ч).
Число М некоторых сверхзвуковых самолетов:
А вот гиперзвуковые летательные аппараты:
SR-71 — самый быстрый серийный самолет
Еще одно замечание, число Маха в авиации, это качественная величина, а не количественная. То есть это не скорость в чистом виде, а критерий который показывает насколько скорость объекта выше скорости звука. Зачем? Затем, что дозвуковые, трансзвуковые, сверхзвуковые или гиперзвуковые скорости очень сильно отличаются по сути.
Пилоту (и инженеру тоже) важно знать какой у него сейчас режим обтекания самолета (дозвуковой, трансзвуковой или сверхзвуковой). Например, во многих указателях скорости есть отдельный циферблат, показывающий значение числа Маха в дополнению к приборной скорости.
На картинке в начале этого повествования изображен трансзвуковой режим. Это значит, что сам самолет еще не превысил скорость звука, а на некоторых его участках (на фото это очень хорошо видно по белым «клиньям») скорость обтекания уже достигла скорости звука.
Поэтому и образовались скачки уплотнения которые хорошо видны благодаря образованию конденсата позади них. Вот почему, число Маха так важно.
Скорость звука
Из Википедии — свободной энциклопедии
| 0 °C, 101325 Па | м/с | км/ч |
|---|---|---|
| Азот | 334 | 1202,4 |
| Аммиак | 415 | 1494,0 |
| Ацетилен | 327 | 1177,2 |
| Водород | 1284 | 4622,4 |
| Воздух | 331 | 1191,6 |
| Гелий | 965 | 3474,0 |
| Кислород | 316 | 1137,6 |
| Метан | 430 | 1548,0 |
| Угарный газ | 338 | 1216,8 |
| Неон | 435 | 1566,0 |
| Углекислый газ | 259 | 932,4 |
| Хлор | 206 | 741,6 |
| Жидкости | ||
| Вода | 1403 | 5050,8 |
| Ртуть | 1383 | 4978,0 |
| Твёрдые тела | ||
| Алмаз | 12000 | 43200,0 |
| Железо | 5950 | 21420,0 |
| Золото | 3240 | 11664,0 |
| Литий | 6000 | 21600,0 |
| Стекло | 4800 | 17280,0 |
Скорость звука — скорость распространения упругих волн в среде: как продольных (в газах, жидкостях или твёрдых телах), так и поперечных, сдвиговых (в твёрдых телах).
Определяется упругостью и плотностью среды: как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях — меньше, чем в твёрдых телах. Также в газах скорость звука зависит от температуры данного вещества, в монокристаллах — от направления распространения волны.
Обычно не зависит от частоты волны и её амплитуды; в тех случаях, когда скорость звука зависит от частоты, говорят о дисперсии звука.
Скорость звука
Полезное
Смотреть что такое «Скорость звука» в других словарях:
Скорость звука — в газах (0 °C; 101325 Па), м/с[1] Азот 334 Аммиак 415 Ацетилен 327 Водород 1284 Воздух 331 Гелий 965 Кислород 316 … Википедия
СКОРОСТЬ ЗВУКА — скорость перемещения в среде упругой волны при условии, что форма её профиля остаётся неизменной. Скорость гармонической волны наз. также фазовой скоростью звука. Обычно С. з. величина постоянная для данного в ва при заданных внеш. условиях и не… … Физическая энциклопедия
СКОРОСТЬ ЗВУКА — скорость распространения звуковых волн в среде. В газах скорость звука меньше, чем в жидкостях, а в жидкостях меньше, чем в твердых телах (причем для сдвиговых волн скорость всегда меньше, чем для продольных). скорость звука в газах и парах от… … Большой Энциклопедический словарь
скорость звука — скорость распространения акустических волн 1. Скорость распространения упругой волны в среде. Единица измерения м/с 2. Фазовая или групповая скорость акустической волны в недисперсионном материале для данного направления распространения. [BS EN… … Справочник технического переводчика
Скорость звука — скорость распространения (относительно среды) малых возмущений давления. В совершенном газе (например, в воздухе при умеренных температурах и давлении) С. з. не зависит от характера распространяющегося малого возмущения и одинакова как для… … Энциклопедия техники
СКОРОСТЬ ЗВУКА — скорость распространения звуковых волн (см. ) в упругих средах (твёрдых телах, жидкостях и газах). Эта скорость зависит (при достаточно малых амплитудах) от механических свойств среды (сжимаемости (см.), (см.), (см.)), не зависит от частоты волны … Большая политехническая энциклопедия
скорость звука — скорость распространения звуковых волн в среде. В газах скорость звука меньше, чем в жидкостях, а в жидкостях меньше, чем в твердых телах (причём для сдвиговых волн всегда меньше, чем для продольных). Скорость звука в газах и парах от 150 до… … Энциклопедический словарь
скорость звука — 2.1.26 скорость звука; скорость распространения ультразвуковой волны: Фазовая или групповая скорость акустической волны в недисперсионном (однородном) материале в направлении распространения. Источник: ГОСТ Р ИСО 5577 2009: Контроль неразрушающий … Словарь-справочник терминов нормативно-технической документации
скорость звука — garso greitis statusas T sritis automatika atitikmenys: angl. sound velocity vok. Schallgeschwindigkeit, f rus. звуковая скорость, f; скорость звука, f pranc. vitesse du son, f … Automatikos terminų žodynas
скорость звука — garso greitis statusas T sritis Energetika apibrėžtis Greitis, kuriuo garsas sklinda tam tikroje aplinkoje arba terpėje. atitikmenys: angl. sonic speed vok. Schallgeschwindigkeit, f rus. звуковая скорость, f; скорость звука, f pranc. célérité du… … Aiškinamasis šiluminės ir branduolinės technikos terminų žodynas
Скорость звука
Скорость звука в идеальном газе зависит только от его температуры и состава. Скорость имеет слабую зависимость от частоты и давления в обычном воздухе, немного отклоняясь от идеального поведения.
Содержание
История [ править ]
Основные понятия [ править ]
Передачу звука можно проиллюстрировать с помощью модели, состоящей из множества сферических объектов, связанных между собой пружинами.
В реальных материальных условиях сферы представляют собой молекулы материала, а пружины представляют собой связи между ними. Звук проходит через систему, сжимая и расширяя пружины, передавая акустическую энергию соседним сферам. Это помогает передавать энергию, в свою очередь, пружинам (связям) соседней сферы и так далее.
Скорость звука в модели зависит от жесткости / жесткости пружины и массы сфер. Пока расстояние между сферами остается постоянным, более жесткие пружины / связи передают энергию быстрее, в то время как более крупные сферы передают энергию медленнее.
Например, звук в никеле распространяется в 1,59 раза быстрее, чем в бронзе, из-за большей жесткости никеля примерно при такой же плотности. Точно так же звук распространяется примерно в 1,41 раза быстрее в газе легкого водорода ( протия ), чем в газе тяжелого водорода ( дейтерия ), поскольку дейтерий имеет аналогичные свойства, но в два раза большую плотность. В то же время звук «компрессионного типа» будет распространяться быстрее в твердых телах, чем в жидкостях, и быстрее в жидкостях, чем в газах, потому что твердые тела сложнее сжимать, чем жидкости, а жидкости, в свою очередь, труднее сжимать. чем газы.
В некоторых учебниках ошибочно утверждается, что скорость звука увеличивается с плотностью. Это понятие проиллюстрировано данными для трех материалов, таких как воздух, вода и сталь, каждый из которых имеет существенно разную сжимаемость, что более чем компенсирует разницу в плотности. Наглядным примером этих двух эффектов является то, что звук в воде распространяется всего в 4,3 раза быстрее, чем в воздухе, несмотря на огромные различия в сжимаемости двух сред. Причина в том, что большая плотность воды, которая замедляет звук в воде по сравнению с воздухом, почти компенсирует разницу в сжимаемости двух сред.
Практический пример можно наблюдать в Эдинбурге, когда «One o’Clock Gun» стреляют в восточной части Эдинбургского замка. Стоя у подножия западной оконечности Касл-Рока, звук ружья можно услышать сквозь скалу, незадолго до того, как он прибудет по воздуху, частично задержанный немного более длинным маршрутом. Это особенно эффективно, если производится салют из нескольких пистолетов, например, «День рождения королевы».
Сжатие и поперечные волны [ править ]
Уравнения [ править ]
Для жидкостей в целом скорость звука c определяется уравнением Ньютона – Лапласа:
Зависимость от свойств среды [ править ]
В газах адиабатическая сжимаемость напрямую связана с давлением через коэффициент теплоемкости (индекс адиабаты), в то время как давление и плотность обратно пропорциональны температуре и молекулярной массе, поэтому важны только полностью независимые свойства температуры и молекулярной структуры (теплоемкость соотношение может определяться температурой и молекулярной структурой, но простой молекулярной массы недостаточно для его определения).
Изменение высоты и значение для атмосферной акустики [ править ]
Практическая формула сухого воздуха [ править ]
Приблизительную скорость звука в сухом (влажность 0%) воздухе в метрах в секунду при температуре около 0 ° C можно рассчитать по формуле
\mathrm
Это уравнение получено из первых двух членов разложения Тейлора следующего более точного уравнения:
\mathrm
Разделив первую часть и умножив вторую часть справа на √ 273,15, мы получим точно эквивалентную форму
\mathrm
который также можно записать как
\mathrm
Подробности [ править ]
Скорость звука в идеальных газах и воздухе [ править ]
Для идеального газа K ( объемный модуль упругости в уравнениях выше, эквивалентный C, коэффициент жесткости в твердых телах) определяется выражением
таким образом, из приведенного выше уравнения Ньютона – Лапласа скорость звука в идеальном газе определяется выражением
Это уравнение применяется только тогда, когда звуковая волна представляет собой небольшое возмущение для условий окружающей среды, и выполняются некоторые другие отмеченные условия, как указано ниже. Было обнаружено, что расчетные значения для c воздух незначительно отличаются от экспериментально определенных значений. [12]
Численная замена приведенных выше значений дает приближение скорости звука для газов в идеальном газе, которое является точным при относительно низких давлениях и плотностях газа (для воздуха это включает стандартные условия на уровне Земли на уровне моря). Также для двухатомных газов использование γ = 1,4000 требует, чтобы газ существовал в диапазоне температур, достаточно высоких, чтобы вращательная теплоемкость была полностью возбуждена (т.е. вращение молекул полностью использовалось в качестве «перегородки» или резервуара тепловой энергии); но в то же время температура должна быть достаточно низкой, чтобы молекулярные колебательные моды не вносили вклад в теплоемкость (т. е. незначительное тепло переходит в вибрацию, поскольку все колебательные квантовые моды выше моды минимальной энергии имеют слишком высокие энергии, чтобы их мог заселить значительное количество молекул при этой температуре). Для воздуха эти условия выполняются при комнатной температуре, а также при температурах значительно ниже комнатной (см. Таблицы ниже). См. Раздел, посвященный газам в удельной теплоемкости, для более полного обсуждения этого явления.
Для воздуха мы вводим сокращение
Подстановка числовых значений
\mathrm
для молярной газовой постоянной в Дж / моль / Кельвин, и
\mathrm
\mathrm
\mathrm
Приведенный выше вывод включает первые два уравнения, приведенные в разделе «Практическая формула для сухого воздуха» выше.
Воздействие сдвига ветра [ править ]
Для распространения звука экспоненциальное изменение скорости ветра с высотой можно определить следующим образом: [16]
В битве при Юке во время Гражданской войны в США в 1862 году акустическая тень, усиленная северо-восточным ветром, не позволила двум дивизиям солдат Союза участвовать в битве [17], потому что они не могли слышать звуки боя всего в 10 км. (шесть миль) по ветру. [18]
Таблицы [ править ]
В стандартной атмосфере :
| Температура T ( ° C ) | Скорость звука c ( м / с ) | Плотность воздуха ρ ( кг / м 3 ) | Характеристический удельный акустический импеданс z 0 ( Па · с / м ) |
|---|---|---|---|
| 35 год | 351,88 | 1,1455 | 403,2 |
| 30 | 349,02 | 1,1644 | 406,5 |
| 25 | 346,13 | 1,1839 | 409,4 |
| 20 | 343,21 | 1,2041 | 413,3 |
| 15 | 340,27 | 1,2250 | 416,9 |
| 10 | 337,31 | 1,2466 | 420,5 |
| 5 | 334,32 | 1,2690 | 424,3 |
| 0 | 331,30 | 1,2922 | 428,0 |
| −5 | 328,25 | 1,3163 | 432,1 |
| −10 | 325,18 | 1,3413 | 436,1 |
| −15 | 322,07 | 1,3673 | 440,3 |
| −20 | 318,94 | 1,3943 | 444,6 |
| −25 | 315,77 | 1,4224 | 449,1 |
При нормальных атмосферных условиях температура и, следовательно, скорость звука зависят от высоты:
Влияние частоты и состава газа [ править ]
Общие физические соображения [ править ]
Среда, в которой распространяется звуковая волна, не всегда реагирует адиабатически, и в результате скорость звука может изменяться с частотой. [19]
Обратите внимание, что в этом примере мы предположили, что температура достаточно низкая, чтобы на теплоемкость не влияла молекулярная вибрация (см. Теплоемкость ). Однако колебательные моды просто вызывают гаммы, которые уменьшаются до 1, поскольку колебательные моды в многоатомном газе дают газу дополнительные способы хранения тепла, которые не влияют на температуру и, таким образом, не влияют на скорость молекул и скорость звука. Таким образом, влияние более высоких температур и колебательной теплоемкости увеличивает разницу между скоростью звука в одноатомных и многоатомных молекулах, при этом скорость остается большей в одноатомных.
Практическое применение в эфире [ править ]
Безусловно, наиболее важным фактором, влияющим на скорость звука в воздухе, является температура. Скорость пропорциональна квадратному корню из абсолютной температуры, что дает увеличение примерно на 0,6 м / с на градус Цельсия. По этой причине высота звука музыкального духового инструмента увеличивается с повышением его температуры.
Скорость звука увеличивается из-за влажности, но уменьшается из-за углекислого газа. Разница между влажностью 0% и 100% составляет около 1,5 м / с при стандартном давлении и температуре, но величина эффекта влажности резко возрастает с температурой. Содержание углекислого газа в воздухе не зафиксировано как из-за загрязнения углеродом, так и из-за человеческого дыхания (например, в воздухе, продуваемом ветровыми инструментами).
Число Маха [ править ]
Число Маха, полезная величина в аэродинамике, представляет собой отношение скорости воздуха к локальной скорости звука. На высоте, по объясненным причинам, число Маха является функцией температуры. Однако летные приборы самолета работают с использованием перепада давления для вычисления числа Маха, а не температуры. Предполагается, что определенное давление представляет собой определенную высоту и, следовательно, стандартную температуру. Летательные приборы самолета должны работать таким образом, потому что давление торможения, измеряемое трубкой Пито, зависит как от высоты, так и от скорости.
Экспериментальные методы [ править ]
Существует ряд различных методов измерения звука в воздухе.
Методы однократного отсчета времени [ править ]
Если источник звука и два микрофона расположены по прямой линии с источником звука на одном конце, то можно измерить следующее:
Другие методы [ править ]
В этих методах, то время измерение было заменено измерением обратного времени ( частоты ).
Высокоточные измерения в воздухе [ править ]
Негазообразные среды [ править ]
Скорость звука в твердых телах [ править ]
Трехмерные тела [ править ]
В твердом теле имеется ненулевая жесткость как для объемных деформаций, так и для деформаций сдвига. Следовательно, можно генерировать звуковые волны с разными скоростями в зависимости от режима деформации. Звуковые волны, вызывающие объемные деформации (сжатие) и сдвиговые деформации (сдвиг), называются волнами давления (продольными волнами) и поперечными волнами (поперечными волнами) соответственно. При землетрясениях соответствующие сейсмические волны называются P-волнами (первичными волнами) и S-волнами (вторичными волнами) соответственно. Скорости звука этих двух типов волн, распространяющихся в однородном трехмерном твердом теле, соответственно задаются формулой [23]
Одномерные тела [ править ]
Скорость звука для волн давления в жестких материалах, таких как металлы, иногда указывается для «длинных стержней» рассматриваемого материала, скорость в которых легче измерить. В стержнях, диаметр которых меньше длины волны, скорость чистых волн давления может быть упрощена и определяется следующим образом: [25]
Скорость звука в жидкостях [ править ]
В жидкости только ненулевая жесткость связана с объемной деформацией (жидкость не выдерживает поперечных сил).
Следовательно, скорость звука в жидкости определяется выражением
Вода [ править ]
Морская вода [ править ]
4 м / с ) и солености (изменение на 1 ‰
1 м / с ) и эмпирических уравнений были получены для точного расчета скорости звука на основе этих переменных. [28] [29] Другие факторы, влияющие на скорость звука, незначительны. Поскольку в большинстве районов океана температура уменьшается с глубиной, профиль скорости звука с глубиной уменьшается до минимума на глубине нескольких сотен метров. Ниже минимума скорость звука снова увеличивается, поскольку эффект увеличения давления преодолевает эффект снижения температуры (справа). [30] Для получения дополнительной информации см. Dushaw et al. [31]
Эмпирическое уравнение для скорости звука в морской воде предоставлено Маккензи: [32]
(Примечание: график зависимости скорости звука от глубины не коррелирует напрямую с формулой Маккензи. Это связано с тем, что температура и соленость различаются на разных глубинах. Когда T и S остаются постоянными, сама формула всегда увеличивается с глубина.)
Другие уравнения для скорости звука в морской воде точны в широком диапазоне условий, но намного сложнее, например, уравнение В.А. Дель Гроссо [33] и уравнение Чена-Миллеро-Ли. [31] [34]
Скорость звука в плазме [ править ]
Скорость звука в плазме в общем случае, когда электроны горячее, чем ионы (но не намного горячее), определяется формулой (см. Здесь )
\mathrm
В отличие от газа, давление и плотность определяются отдельными компонентами, давление электронами и плотность ионами. Они связаны через колеблющееся электрическое поле.
Градиенты [ править ]
Когда звук распространяется равномерно во всех направлениях в трех измерениях, интенсивность падает пропорционально обратному квадрату расстояния. Однако в океане есть слой, называемый «глубокий звуковой канал» или канал SOFAR, который может удерживать звуковые волны на определенной глубине.
Аналогичный эффект происходит в атмосфере. Проект «Могул» успешно использовал этот эффект для обнаружения ядерного взрыва на значительном расстоянии.