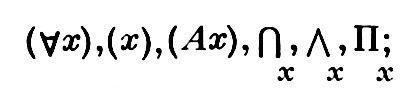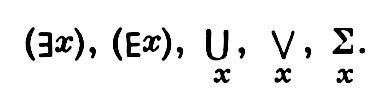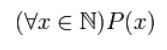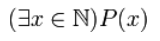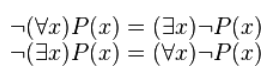Что такое слова кванторы

КВАНТОР

Полезное

Смотреть что такое «КВАНТОР» в других словарях:

квантор — сущ., кол во синонимов: 1 • оператор (24) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

квантор — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN quantifier … Справочник технического переводчика

КВАНТОР — общее название для логических операций, к рые по предикату Р(х)строят высказывание, характеризующее область истинности предиката Р(х). В математич. логике наиболее употребительны квантор всеобщности и квантор существования Высказывание означает,… … Математическая энциклопедия

Квантор — (от лат. quantum сколько) символ, используемый для обозначения некоторых операций математической логики, одновременно логическая операция, дающая количественную характеристику области предметов, к которым относится выражение, получаемое в… … Начала современного естествознания

квантор — а, ч., лог. Логічний оператор, який переводить одну висловлювальну форму в іншу. Квантор існування … Український тлумачний словник

квантор — kvantorius statusas T sritis automatika atitikmenys: angl. quantifier vok. Quantor, m rus. квантор, m pranc. quantifier, m … Automatikos terminų žodynas

Квантор — (от лат. quantum сколько) логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате её применения. В обычном языке носителями таких характеристик служат слова типа… … Большая советская энциклопедия

квантор — кв антор, а … Русский орфографический словарь

Источник

Значение слова «квантор»

Квантор всеобщности (обозначение:

, читается: «для любого…», «для каждого…», «для всех…» или «каждый…», «любой…», «все…»).

Квантор существования (обозначение:

, читается: «существует…» или «найдётся…»).

В математической логике приписывание квантора к формуле называется связыванием или квантификацией.

В многозначных логиках также вводятся и другие кванторы, например, квантор плюральности (квантор Решера) (обозначается перевёрнутой M, читается «для большинства …»).

ква́нтор

1. лог. филос. общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих высказывание

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: аршин — это что-то нейтральное, положительное или отрицательное?

Ассоциации к слову «квантор&raquo

Синонимы к слову «квантор&raquo

Предложения со словом «квантор&raquo

Сочетаемость слова «квантор&raquo

Понятия, связанные со словом «квантор»

Отправить комментарий

Дополнительно

Предложения со словом «квантор&raquo

Задачи 2.1, 2.2 и 2.13 помогают разобраться в способах передачи кванторов общности и существования средствами русского языка.

А в бытовом языке вместо кванторов используют самые разные слова, что порой приводит к недоразумениям.

Так, применённый к понятию, квантор существования означает, что при подстановке по крайней мере одного имени предмета это понятие превращается в предложение, имеющее в качестве истинностного значения «истину», т. е., иными словами, это понятие не является пустым.

Источник

Квантор

Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката и создающих выcказывание. Чаще всего упоминают:

В математической логике приписывание квантора к формуле называется связыванием или квантификацией.

В многозначных логиках также вводятся и другие кванторы, например, квантор плюральности (квантор Решера) (обозначается перевёрнутой M, читается «для большинства …»).

Содержание

Примеры

Обозначим предикат «x делится на 5». Используя квантор общности, можно формально записать следующие высказывания (конечно, ложные):

.

Следующие (уже истинные) высказывания используют квантор существования:

Их формальная запись:

.

Введение в понятие

Пусть на множестве простых чисел задан предикат : «Простое число нечётно». Подставим перед этим предикатом слово «любое». Получим ложное высказывание «любое простое число нечётно» (это высказывание ложно, так как 2 — простое чётное число).

Подставив перед данным предикатом слово «существует», получим истинное выcказывание «Существует простое число , являющееся нечётным» (например, ).

Таким образом, превратить предикат в высказывание можно, поставив перед предикатом слова («все», «существует» и другие), называемые в логике кванторами.

Кванторы в математической логике

(«При всех значениях (x) утверждение верно»).

(«Существует (x) при котором утверждение верно»).

Свободные и связанные переменные

Множество свободных переменных* формулы F определяется рекурсивно, следующим образом:

Связанное переименование, свободное переименование

Операции над кванторами

Правило отрицания кванторов — применяется для построения отрицаний высказываний, содержащих кванторы, и имеет вид:

История появления

Философы давно обращали внимание на логические операции, ограничивающие область истинности предиката, однако не выделяли их в отдельный класс операций. Так, Томас Гоббс считал, что они являются частями имен. [1]

Хотя кванторно-логические конструкции широко используются как в научной, так и в обыденной речи, их формализация произошла только в 1879 г., в книге Фреге «Исчисление понятий». Обозначения Фреге имели вид громоздких графических конструкций и не были приняты. Впоследствии было предложено множество более удачных символов, но общепринятыми стали обозначения для квантора существования (перевёрнутая первая буква англ. Exists — существует), предложенное Чарльзом Пирсом в 1885 г., и для квантора общности (англ. All — все), образованное Герхардом Генценом в 1935 г. по аналогии с символом квантора существования. Термины «квантор», «квантификация» также предложил Пирс.

Литература

Ссылки

Примечания

Полезное

Смотреть что такое «Квантор» в других словарях:

КВАНТОР — логический оператор, с помощью которого высказывание о к. л. отдельном объекте преобразуется в высказывание о совокупности (множестве) таких объектов. В логике используется два основных К.: К. общности, «V», и К. существования, «Э». В… … Философская энциклопедия

квантор — сущ., кол во синонимов: 1 • оператор (24) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов

квантор — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN quantifier … Справочник технического переводчика

КВАНТОР — общее название для логических операций, к рые по предикату Р(х)строят высказывание, характеризующее область истинности предиката Р(х). В математич. логике наиболее употребительны квантор всеобщности и квантор существования Высказывание означает,… … Математическая энциклопедия

Квантор — (от лат. quantum сколько) символ, используемый для обозначения некоторых операций математической логики, одновременно логическая операция, дающая количественную характеристику области предметов, к которым относится выражение, получаемое в… … Начала современного естествознания

квантор — а, ч., лог. Логічний оператор, який переводить одну висловлювальну форму в іншу. Квантор існування … Український тлумачний словник

квантор — kvantorius statusas T sritis automatika atitikmenys: angl. quantifier vok. Quantor, m rus. квантор, m pranc. quantifier, m … Automatikos terminų žodynas

Квантор — (от лат. quantum сколько) логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате её применения. В обычном языке носителями таких характеристик служат слова типа… … Большая советская энциклопедия

квантор — кв антор, а … Русский орфографический словарь

Источник

Логические операции. Кванторы

Логические операции

В любом национальном языке употребляемые в обычной речи связки “и”, “или”, “если …, то …”, “тогда и только тогда, когда …” и т.п. позволяют из уже заданных высказываний строить новые сложные высказывания. Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями. Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает сложное высказывание при всех возможных значениях простых высказываний.

Логической операцией называется способ построения сложного высказывания из элементарных высказываний, при котором истинностное значение сложного высказывания полностью определяется истинностными значениями исходных высказываний (см. статью “Высказывания. Логические значения”).

В алгебре логики логические операции и соответствующие им логические связки имеют специальные названия и обозначаются следующим образом:

Рассмотрим два высказывания: p = “Колумб был в Индии” и q = “Колумб был в Египте”. Очевидно, что новое высказывание p q = “Колумб был в Индии или был в Египте” истинно как в случае, если Колумб был в Индии, но не был в Египте, так и в случае, если он не был в Индии, но был в Египте, а также в случае, если он был и в Индии, и в Египте. Но это высказывание будет ложно, если Колумб не был ни в Индии, ни в Египте.

Союз “или” может применяться в речи и в другом, “исключающем” смысле. Тогда он соответствует другому высказыванию — разделительной, или строгой, дизъюнкции.

Строгая, или разделительная, дизъюнкция — логическая операция, ставящая в соответствие двум элементарным высказываниям новое высказывание, являющееся истинным только тогда, когда только одно из высказываний является истинным. Логическая операция разделительная дизъюнкция определяется следующей таблицей истинности:

Рассмотрим два высказывания: p = “Кошка охотится за мышами” и q = “Кошка спит на диване”. Очевидно, что новое высказывание p q истинно только в двух случаях — когда кошка охотится за мышами либо когда кошка мирно спит. Это высказывание будет ложно, если кошка не делает ни того, ни другого, т.е. когда оба события не происходят. Но это высказывание будет ложным и тогда, когда предполагается, что оба высказывания произойдут одновременно. В силу того, что этого произойти не может, высказывание и является ложным.

В логике связкам “либо” и “или” придается разное значение, однако в русском языке связку “или” иногда употребляют вместо связки “либо”. В этих случаях однозначность определения используемой логической операции связана с анализом содержания высказывания. Например, анализ высказывания “Петя сидит на трибуне А либо на трибуне Б” заменить на “Петя сидит на трибуне А или Б”, то анализ последнего высказывания однозначно укажет на логическую операцию разделительная дизъюнкция, т.к. человек не может находиться в двух разных местах одновременно.

Импликация — логическая операция, ставящая в соответствие каждым двум элементарным высказываниям новое высказывание, являющееся ложным тогда и только тогда, когда условие (посылка) — истинно, а следствие (заключение) — ложно. Подавляющее число зависимостей между событиями можно описать с помощью импликации. Например, высказыванием “Если на каникулах мы поедем в Петербург, то посетим Исаакиевский собор” мы утверждаем, что в случае приезда на каникулах в Петербург Исаакиевский собор мы посетим обязательно.

Логическая операция импликация задается следующей таблицей истинности:

Импликация будет ложной только тогда, когда посылка истинна, а заключение ложно, и она заведомо будет истинна, если ее условие p ложно. Причем для математика это вполне естественно. В самом деле, исходя из ложной посылки, можно путем верных рассуждений получить как истинное, так и ложное утверждение.

Допустим, 1 = 2, тогда и 2 = 1. Складывая эти равенства, мы получим 3 = 3, т.е. из ложной посылки путем тождественных преобразований мы получили истинное высказывание.

Импликация, образованная из высказываний А и В, может быть записана при помощи следующих предложений: “Если А, то В”, “Из А следует В”, “А влечет В”, “Для того чтобы А, необходимо, чтобы В”, “Для того чтобы В, достаточно, чтобы А”.

Эквивалентность — логическая операция, ставящая в соответствие двум элементарным высказываниям новое, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны. Логическая операция эквивалентность задается следующей таблицей истинности:

Рассмотрим возможные значения сложного высказывания, являющегося эквивалентностью: “Учитель поставит ученику 5 в четверти тогда и только тогда, когда ученик получит 5 на зачете”.

1) Ученик получил 5 на зачете и 5 в четверти, т.е. учитель выполнил свое обещание, следовательно, высказывание является истинным.

2) Ученик не получил на зачете 5, и учитель не поставил ему 5 в четверти, т.е. учитель свое обещание сдержал, высказывание является истинным.

3) Ученик не получил на зачете 5, но учитель поставил ему 5 в четверти, т.е. учитель свое обещание не сдержал, высказывание является ложным.

4) Ученик получил на зачете 5, но учитель не поставил ему 5 в четверти, т.е. учитель свое обещание не сдержал, высказывание является ложным.

Отметим, что в математических теоремах эквивалентность выражается связкой “необходимо и достаточно”.

Рассмотренные выше операции были двухместными (бинарными), т.е. выполнялись над двумя операндами (высказываниями). В алгебре логики определена и широко применяется и одноместная (унарная) операция отрицание.

Отрицание — логическая операция, которая каждому элементарному высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному. Логическая операция отрицание задается следующей таблицей истинности:

В русском языке для построения отрицания используется связка “неверно, что …”. Хотя связка “неверно, что …” и не связывает двух каких-либо высказываний в одно, она трактуется логиками как логическая операция, поскольку, поставленная перед произвольным высказыванием, образует из него новое.

Отрицанием высказывания “У меня дома есть компьютер” будет высказывание “Неверно, что у меня дома есть компьютер” или, что в русском языке то же самое, “У меня дома нет компьютера”. Отрицанием высказывания “Я не знаю китайского языка” будет высказывание “Неверно, что я не знаю китайского языка” или, что в русском языке одно и то же, “Я знаю китайский язык”.

Кванторы

В математической логике наряду с логическими операциями используются и кванторы. Квантор (от лат. quantum — сколько) — логическая операция, дающая количественную характеристику области предметов, к которой относится выражение, получаемое в результате ее применения.

В обычном языке носителями таких характеристик служат слова типа все, каждый, некоторый, любой, всякий, бесконечно много, существует, имеется, единственный, несколько, конечное число, а также все количественные числительные. В формализованных языках, составной частью которых является исчисление предикатов, для выражения всех подобных характеристик оказывается достаточным кванторов двух видов: квантора общности и квантора существования.

Квантор общности позволяет из данной высказывательной формы с единственной свободной переменной x получить высказывание с помощью связки “Для всех x …”. Результат применения квантора общности к высказывательной форме A(x) обозначают x A(x). Высказывание x A(x) будет истинным тогда и только тогда, когда при подстановке в A(x) вместо свободной переменной x любого объекта из области возможных значений всегда получается истинное высказывание. Высказывание x A(x) может читаться следующим образом: “Для любого x имеет место A(x)”, “A(x) при произвольном x”, “Для всех x верно A(x)”, “Каждый x обладает свойством A(x)” и т.п.

Квантор существования позволяет из данной высказывательной формы с единственной свободной переменной x получить высказывание с помощью связки “Существует такой x, что …”. Результат применения квантора общности к высказывательной форме A(x) обозначают x A(x). Высказывание
x A(x) истинно тогда и только тогда, когда в области возможных значений переменной x найдется такой объект, что при подстановке его имени вместо вхождения свободной переменной x в A(x) получается истинной высказывание. Высказывание x A(x) может читаться следующим образом: “Для некоторого x имеет место A(x)”, “Для подходящего x верно A(x)”, “Существует x, для которого A(x)”, “Хотя бы для одного x верно A(x)” и т.п.

Кванторы играют для формализованных языков математической логики ту же роль, которую играют для естественного языка так называемые “количественные” (“кванторные”) слова, — определяют область применимости данного высказывания (или высказывательной формы).

При построении отрицания к высказыванию, содержащему квантор, действует следующее правило: частица “не” добавляется к сказуемому, квантор общности заменяется на квантор единственности и наоборот. Рассмотрим пример. Отрицанием высказывания “Все юноши 11-х классов — отличники” является высказывание “Неверно, что все юноши 11-х классов — отличники” или “Некоторые юноши 11-х классов — не отличники”.

В информатике кванторы применяются в логических языках программирования (см. “Языки программирования”) и языках запросов к базам данных.

Методические рекомендации

Умение строить сложные высказывания требуется при работе с базами данных, при конструировании запроса поиска в Интернете, при построении алгоритмов и написании программ на любом алгоритмическом языке. Более того, это умение можно отнести к общешкольным умениям, т.к. оно связано с построением сложных умозаключений (рассуждений, получений выводов). В основе этого умения лежат знание основных логических операций и умение определять истинность сложных высказываний.

С логическими операциями дизъюнкция, конъюнкция и отрицание школьники знакомятся в основной школе. Там же вводится и понятие таблицы истинности. Скорее всего знакомство с данными понятиями возникает в языках программирования, но использовать их можно и в электронных таблицах — там логические операции реализованы через соответствующие функции OR, AND, NOT.

Более сложные логические операции могут быть рассмотрены в старшей школе. Задачи, использующие импликацию, встречаются в каждом из опубликованных вариантов ЕГЭ по информатике. Например: для какого числа X истинно высказывание ((X > 3) (X (X

6 От латинских слов idem — тот же самый и potens — сильный; дословно — равносильный.

7 Это определение легко распространяется на случай n высказываний (n > 2, n — натуральное число).

8 Это определение, как и предыдущее, распространяется на случай n высказываний (n > 2, n — натуральное число).

9 Успенский В.А., Верещагин Н.К., Плиско В.Е. Вводный курс математической логики. М.: Физматлит, 2002.

Источник

Предикаты и кванторы

Вы будете перенаправлены на Автор24

Понятие предиката

Предикатом в программировании является функция, которая принимает один или более аргументов и возвращает значения булева типа.

Предикат называется тождественно-истинным, если на любом наборе аргументов он принимает истинное значение:

Предикат называется тождественно-ложным, если на любом наборе аргументов он принимает ложное значение:

Предикат называется выполнимым, если хотя бы на одном наборе аргументов он принимает истинное значение.

Примеры предикатов

Таким образом, предикатом является все то, что утверждается или отрицается о субъекте суждения.

Готовые работы на аналогичную тему

Операции над предикатами

Рассмотрим применение операций алгебры логики к предикатам.

Логические операции:

Над предикатами помимо логических операций можно выполнять квантовые операции: применение квантора всеобщности, квантора существования и т.д.

Кванторы

Чаще всего используют кванторы:

В математической логике существует понятие связывание или квантификация, которые обозначают приписывание квантора к формуле.

Примеры применения кванторов

С помощью квантора всеобщности можно записать следующие ложные высказывания:

который будет иметь вид:

Для записи истинных высказываний используем квантор существования:

Запись будет иметь вид:

Таким образом, предикат можно превратить в высказывание, если поставить перед предикатом квантор.

Операции над кванторами

Для построения отрицания высказываний, которые содержат кванторы, применяется правило отрицания кванторов:

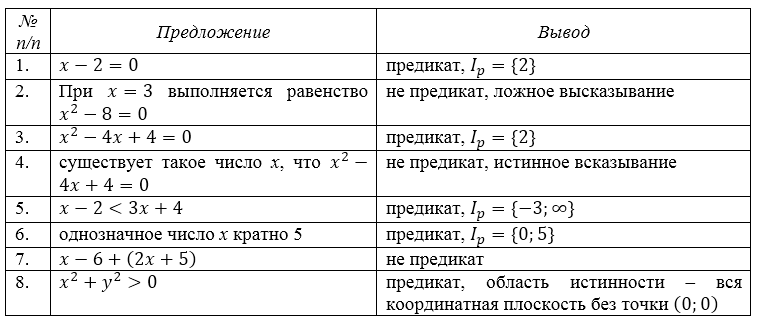
Рассмотрим предложения и выделим среди них предикаты, указав область истинности каждого из них:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата написания статьи: 07 04 2016

Источник