Что такое свойство сложения
Свойства сложения и вычитания
Свойства (или законы) арифметических действий на числовых примерах мы рассматривали в теме «Законы арифметики» для начальной школы.
В 5 классе законы арифметики записываются с помощью буквенных выражений. Поэтому теперь мы рассмотрим эти и другие свойства в виде буквенных выражений.
Свойства сложения
Переместительное свойство сложения
От перестановки слагаемых сумма не меняется.
В буквенном виде свойство записывается так:
Сочетательное свойство сложения
Чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего числа.
Так как результат сложения трёх чисел не зависит от того как поставлены скобки, то скобки можно не ставить и писать просто « a + b + с ».
Переместительное и сочетательное свойство сложения позволяют сформулировать правило преображения сумм.
При сложении нескольких чисел их можно как угодно объединять в группы и переставлять.
Свойство нуля при сложении
Сумма двух натуральных чисел всегда больше каждого из слагаемых. Но это не так, если хотя бы одно из слагаемых равно нулю.
Если к числу прибавить нуль, получится само число.
Свойства вычитания
Свойство вычитания суммы из числа
Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое и затем из результата вычесть другое слагаемое.
Скобки в выражении « (a − b) − c » не имеют значения и их можно опустить.
Свойство вычитания числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
Свойство нуля при вычитании
Если из числа вычесть нуль, получится само число.
Если из числа вычесть само число, то получится нуль.
Базовые свойства
Главными элементами сложения являются аргументы (слагаемые). Сумма — результат увеличения значений первого и второго аргументов. На письме эта математическая операция обозначается символом +. Основными свойствами сложения в математике являются:
Базовые свойства сложения изучаются в начальной школе со 2 класса. Процесс обучения начинается с простых заданий с двумя компонентами, представленными натуральными числами. По мере обучения увеличивается сложность задач и количество слагаемых. В школе большинство вычислений производится в десятичной системе счисления, поэтому в качестве памятки рекомендуется предоставить ученикам таблицу сложения, где представлены суммы пар чисел от 1 до 10.
Нахождение суммы многозначных чисел
Многозначными называются числа, состоящие из двух и более цифр. Для нахождения их суммы необходимо знание численных разрядов. Цифра, стоящая последней, показывает количество единиц. Далее идут десятки, сотни, тысячи, десятки тысяч, сотни тысяч и миллионы. Многозначные числа складываются столбиком. Сложить можно только одинаковые разряды.
Пример: найти сумму многозначных чисел 125 и 234. Отдельно складываются единицы, десятки и сотни: 5 + 4 = 9, 2 + 3 = 5, 1 + 2 = 3. Суммой является число 359.
Для проверки правильности вычислений нужно вычесть из суммы одно из слагаемых. Если разность равна второму слагаемому, то пример решен правильно. Проверку можно осуществить также при помощи калькулятора или иных вычислительных устройств.
Прибавление дробей и смешанных значений
Дробь — часть от целого числа, записываемая в виде x / y. Значение x называется числителем, y — знаменателем. Дробное число представляет собой операцию деления, где делимым является числитель, а делителем — знаменатель. Дробь считается правильной, если числитель не больше знаменателя.
При складывании дробей с одинаковыми знаменателями необходимо прибавлять только их числители (например, 1/5 + 3/5 = 4/5). Если значения, стоящие под знаком дроби, разные, то необходимо привести выражение к единому знаменателю:
Для упрощения этой процедуры рекомендуется приобрести таблицу умножения. С ее помощью можно легко найти общий знаменатель и дополнительные множители.
Десятичной называется дробь, знаменатель которой равен 10. Она состоит из целой и дробной частей, отделенных запятой. При нахождении суммы десятичные дроби записываются столбиком. Важно, чтобы запятые находились на одном уровне. При неравном количестве разрядов с правой стороны дописываются нули. Если в результате после запятой стоит 0, то он опускается.
Смешанное число — сумма обыкновенной дроби (дробная часть) и целого числа (целая часть).
Для определения суммы чисел в смешанной записи необходимо отделить целую часть от дроби и сложить их по отдельности, применяя базовые свойства сложения. Если в результате вычислений получилась неправильная дробь, то нужно следовать следующему алгоритму действий:
В математике процесс преобразования неправильной дроби в смешанное число называется выделением целой части. Если числитель полностью делится на знаменатель, то неправильную дробь можно записать в виде целого числа.
Складывание векторов, пределов и матриц
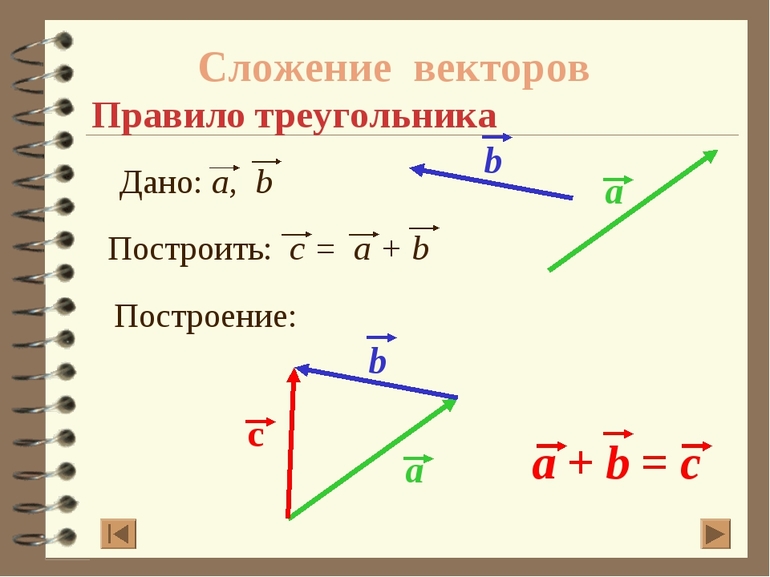
Вектор — отрезок, имеющий длину и направление. Он является одним из основополагающих понятий линейной алгебры. В буквенном виде он записывается двумя заглавными символами латинского алфавита или одной маленькой латинской буквой. Существует два основных способа сложения векторов:
Для нахождения суммы трех и более векторов необходимо отметить на плоскости произвольную точку и последовательно отложить от нее исходные векторы. Отрезок, соединяющий начало первого вектора и конец последнего, является суммой. При сложении важно учитывать, что результат сложения противоположно направленных векторов равен 0. Наглядно способы нахождения суммы векторов проиллюстрированы ниже.
Пределом функции является число, к которой стремится значение функции f (x) при стремлении ее аргумента к заданной точке на графике. Является одним из разделов математического анализа. Предел функции вычисляется по следующей формуле: limx →∞ f (x)= C, где C — число, к которому стремится аргумент функции. Для нахождения предела суммы необходимо сложить функции, стремящиеся к идентичным точкам на заданном графике.
Матрица — элемент высшей математики, представленный в виде таблицы прямоугольной формы. Она состоит из неограниченного количества строк и столбцов, где записываются целые, действительные, иррациональные и комплексные числа. В квадратных матрицах количество столбцов и строк совпадает. Нулевой называется таблица, где все компоненты равны 0. Матрицы нашли применение в записи алгебраических и дифференциальных уравнений.
Складывать можно только одноразмерные матрицы (число строк и столбцов совпадает). В противном случае может измениться их исходный размер. При нахождении суммы матриц каждые элементы складываются по отдельности. Нельзя сложить компоненты, находящиеся в разных строках или столбцах. В результате получится матрица с исходным размером. При сложении применяются свойства коммутативности и ассоциативности. Для складывания нулевых матриц важно знать правило нейтрального элемента.
Сложение в двоичной системе счисления
В двоичной системе счисления математические операции выполняются на электронно-вычислительных машинах. В ней применяются только две цифры: 0 и 1. Сложение в этой системе счисления выполняется в столбик. Для вычислений требуется следующая таблица:
| Условие математической операции |
| 0 + 0 = 0 |
| 0 + 1 = 1 |
| 1 + 0 = 1 |
| 1 + 1 = 10 |
Числа, записываемые в столбик, выравниваются по разделителю целой и дробной частей. Если количество разрядов не совпадает, то с правой стороны необходимо добавить нули. При складывании нескольких чисел возможен перенос через 2 и более разряда.
Для упрощения математической операции можно перевести числа из двоичной системы счисления в десятичную. Для этого над каждой цифрой исходного числа слева направо ставится степень, начиная от 0. Каждый элемент умножается на цифру 2, возведенную в соответствующую степень. Результаты вычислений суммируются. С помощью этого способа можно также переводить в восьмеричную и шестнадцатеричную системы счисления.
Свойства сложения
Содержание
Мы уже умеем складывать числа с помощью рисунка и координатного луча. Умеем складывать однозначные числа, такие как 7 и 5, и многозначные, такие как 123 и 456.
Для того чтобы складывать числа было легче, существует несколько простых правил. Их еще называют законами сложения или свойствами.
Закон – это что-то, что никогда не меняется, и что можно применять для всех чисел.
Заучивать законы сложения не нужно, их нужно только один раз понять и научиться использовать в примерах и задачах. Сделать это очень просто. Сейчас мы сможем в этом убедиться.
Переместительное свойство
Первый закон сложения называется переместительным законом сложения. Звучит он так:
От перестановки слагаемых сумма не меняется.
Чтобы понять этот закон, мы решим один и тот же пример двумя способами.
А теперь поменяем наши числа местами и посчитаем ответ:
Результаты сложения получились одинаковыми. Но заметим, что во втором случае посчитать было гораздо проще, не так ли? Значит, проще было поменять числа местами и потом посчитать.
Сложение с нулем
В корзине было 100 яблок, туда положили 0 яблок, сколько яблок стало в корзине?
Очевидно, что если в корзину не положили яблок, то количество яблок в ней не изменилось, то есть по-прежнему равно 100.
От прибавления нуля число не изменяется
$10+0 = 10$
$0 + 8 = 8$
$0 + 0 = 0$
Сочетательное свойство
В некоторых примерах бывает нужно сложить не два числа, а несколько.
Складываем все числа слева направо привычным для нас способом. Получаем:
Если мы внимательно посмотрим на числа, то сможем увидеть, что легче сначала сложить 4 и 6, а затем к полученной сумме прибавить и число 29.
$29 + 4 + 6 = 24 + 10 = 39$
Ответ получился таким же.
Значит, при сложении нескольких чисел можно складывать сначала те числа, которые нам удобнее сложить. А затем уже к полученной сумме прибавляем оставшиеся числа. Мы, так сказать, сочетаем те числа, которые легче посчитать при сложении.
Этот закон называется сочетательный закон сложения. Кратко он звучит так:
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.
Законы сложения можно применять при сложении не только двух или трех, но и большего количество чисел.
Чтобы решить этот пример, посмотрим внимательно на числа. Заметим, что легче всего было бы сложить 128 и 12, а к числу 383 легче прибавить 17. Поэтому мы сейчас поменяем местами числа 17 и 12. То есть применим в нашем примере переместительный закон. Получим:
Теперь группируем попарно числа, которые будем складывать. То есть применим сочетательный закон. Для этого мы используем скобки:
Считаем, сколько получится в скобках и складываем результаты:
Вот так легко и быстро мы получили ответ, применяя законы сложения.
Свойства сложения

Всего получено оценок: 288.
Всего получено оценок: 288.
Свойства сложения и вычитания – это простейшие действия арифметики. В курсе математике 6 класса свойства изучаются более подробно. Имеет смысл поговорить о каждом свойстве в отдельности, чтобы в дальнейшем не возникало проблем с преобразованием выражений.
Сложение
Сложение – это простейшее свойство математики. Суть сложения заключается в том, что количество единиц одного слагаемого и количество единиц другого слагаемого объединяются в одно число. Это простейшее определение из тех, что может предложить современный курс математики.
Переместительное
Переместительно свойство сложения заключается в знаменитой на всю Россию фразе: «От перемены мест слагаемых сумма не меняется».
Разберемся подробнее в том, почему это свойство называется именно переместительным. Запишем выражение:
а+в=с – вроде бы все в нем понятно, есть первое слагаемое, второе и сумма. Но что будет, если слагаемые поменять местами?
в+а=с – первое и второе слагаемое стали совершенно разными числами, но результат не изменился. Мы переместили слагаемые, именно поэтому свойство и называется переместительным.
Сочетательное
Второе свойство называется сочетательным. Формулировка звучит так: При сложении трех чисел, нет разницы: сложить первые два слагаемых и прибавить к нему третье или наоборот: сложить последние два слагаемых и прибавить к ним первое.
Второе свойство проистекает из первого, расширяясь с двух слагаемых до трех. Разберемся подробнее. Представим сумму из трех слагаемых:
Согласно второму свойству нет разницы выполнить сложение примера так:
Скобки указывают на порядок выполнения действий. То есть нет разницы сложить первые два слагаемых и к нему прибавить третье или сложить вторые два слагаемых и к ним прибавить первые.
Свойство называется сочетательным, потому что нет разницы, как сочетать слагаемые в примере.
Свойство нуля
Первым и основным принципом проверки правильности выполненного сложения является условие: сумма всегда больше каждого из слагаемых.
Это правило было выведено в Индии до того, как придумали число ноль, как отсутствие какого-либо значения в принципе. Поэтому сегодня говорят, что сумма всегда больше каждого из слагаемых, если какое-либо из слагаемых не равно нулю
Если представить себе сумму из двух слагаемых, одно из которых равно нулю, то сумма будет равняться слагаемому неравному нулю:
В некоторых учебниках составляют таблицы свойств сложения для лучшего понимания темы.
Что мы узнали?
Мы поговорили о простейших свойствах сложения. Узнали, почему каждое свойство имеет такое название, и поговорили о первом правиле проверке сложения.
Сложение натуральных чисел
Пройти тест по теме «Сложение и вычитание натуральных чисел» можно по ссылке. Проверьте свои знания!
Сумма чисел – это такое число, которое получается после объединения всех единиц других данных натуральных чисел.
Слагаемые – это числа, над которыми мы выполняем действие сложения. Иными словами, это те числа, количество единиц которых мы объединяем в новом числе.
Арифметическое действие – это нахождение нового числа при помощи двух или нескольких других данных чисел.
В курсе математики 5 класса изучаются основные арифметические действия – сложение, вычитание, умножение и деление.
Сложение – это арифметическое действие, которое выполняется для получения суммы нескольких чисел.
Или другими словами:
Сложение – это действие увеличения числа на количество единиц, содержащихся в другом числе.
Сумма – это результат действия сложения.
Компоненты действия сложения для двух слагаемых:
Компоненты сложения для трех слагаемых:
Рисунок 1. Сумма двух чисел на координатном луче.
Основные свойства суммы натуральных чисел
Переместительный закон сложения
Сумма двух или нескольких чисел от изменения порядка сложения слагаемых не меняется.
Это значит, что значение суммы не зависит от порядка выполнения действия сложение.
Сочетательный закон сложения
Сумма нескольких чисел не поменяется, если некоторые слагаемые заменить их суммой.
Это значит, что мы можем группировать слагаемые как угодно, а также выполнять действия сложения в любом порядке.
Например, если в нашем примере мы заменим слагаемые 2 и 3 их суммой, то результат останется такой же, как и при обычном сложении слагаемых:
или
или
Для прибавления суммы некоторых чисел к числу или некоторого числа к сумме чисел, нужно сложить это число с одним из слагаемых суммы, а получившийся результат сложить последовательно с остальными слагаемыми.
Пример 1. Прибавление числа к сумме чисел:
Можно сразу вычислить сумму чисел в скобках и сложить ее с первым слагаемым:
325 +( 12 + 64 + 5 ) = 325 +81 = 406
Также можно использовать правило прибавления слагаемого и суммы. Результат при этом не поменяется
Пример 2. Прибавление суммы чисел к другому числу:
Можно сразу вычислить сумму чисел в скобках и сложить ее со вторым слагаемым
( 54 + 240 + 189 )+ 37 = 483+ 37 = 520
Или можно использовать правило прибавления суммы чисел к числу. Результат останется тот же.
Изменение суммы чисел с изменением слагаемых
При увеличении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже увеличится на это же число (на это же количество единиц).
При уменьшении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже уменьшится на это же число (на это же количество единиц).
Эти два свойства справедливы и в обратную сторону. То есть, если увеличить или уменьшить сумму на какое-то число, тогда для сохранения равенства нужно соответственно увеличить или уменьшить одно из слагаемых.
Простой пример увеличения суммы при увеличении слагаемого: у вас есть 700 рублей; 200 рублей лежит в левом кармане, а 500 – в правом. Вы нашли на улице 300 рублей и положили их в левый карман, после чего там стало 200+300=500 рублей. Таким образом, всего у вас оказалось 500+500=1000 рублей, то есть, сумма всех ваших денег увеличилась на 300 рублей.
Попробуйте самостоятельно придумать примеры для всех трех правил.
Сложение однозначных чисел
Сложение двух однозначных чисел выполняется так: одно число увеличивается на количество единиц другого числа. То есть, единицы одного числа присоединяются к единицам другого числа.
Сложение многозначного числа с однозначным
Чтобы найти сумму многозначного числа и однозначного, можно действовать двумя способами. Оба они основаны на свойствах суммы чисел. Рассмотрим их на примерах.
То есть, мы проделываем такие действия:
88+5 = 80+8+5 = 80+13 = 80+10+3 = 90+3=93.
То есть, ход вычисления был такой:
88+5 = 88+2+3 = 90+3 = 93.
Сложение в столбик многозначных чисел
Сложение в столбик – это способ нахождения суммы чисел путем их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим).
Итак, допустим, что нам нужно найти сумму : 5728+803
После нахождения суммы чисел методом сложения столбиком, записываем результат решения в исходном строчном примере:
5728+803 = 6531
Сложение в столбик нескольких многозначных чисел
Рассмотрим пример: 12044+28609+1358
Сложив простые единицы, мы получим 21, то есть, 2 десятка и 1 единицу. Записываем под чертой в разряде единиц цифру 1, а 2 отмечаем «в уме».
Нам остается только записать результат в начальном примере:
12044+28609+1358