Формула расчета нагрузки на ось грузового автомобиля

Как рассчитать нагрузку на ось грузового автомобиля

Автомобиль с перегрузом, неважно легковой или фура, – представляет существенную угрозу для всех участников движения. Во-первых, потому что сама машина движется нестабильно. Во-вторых, большая нагрузка на ось может привести к её внезапной поломке. В-третьих, тормозной путь такого авто более длинный, что может привести к аварии. Кроме того, превышение допустимого веса ведёт к разрушению дорожного полотна и мостовых конструкций. И за перегруз полагается административный штраф.

Поэтому в этой статье мы расскажем о нормах предельно допустимой нагрузки на ось грузового автомобиля и о том, как её определить.

Расчёт нагрузки на ось грузового автомобиля

Процесс грузоперевозок регламентируется нормативно-правовыми актами. Среди которых ФЗ об автодорогах №257-ФЗ от 08.11.2007. В соответствии с п. 2 ст. 31 которого для передвижения по автодорогам транспорта с превышением общей допустимого веса или нагрузки на ось больше чем на 2% необходимо получить разрешение. Исключение делается лишь для автотранспорта Вооружённых сил России.
При получении разрешения владелец авто должен:

Компенсировать урон, наносимый покрытию дороги.

Если перегруз менее 10%, используется упрощённая процедура выдачи, которая занимает всего 1 день.

Кроме того, проезд по мостам и участкам дороги иногда бывает ограничен специальными знаками, указывающим предельное значение веса грузового автомобиля или нагрузки на его ось. Это может быть связано с грузоподъёмностью конструкции или её состоянием.

Полный список документов, необходимых для оформления карты

Максимально допустимая нагрузка на ось грузовых автомобилей в России

Постановлением Правительства Российский Федерации о правилах перевозки грузов автотранспортом установлен допустимый предельный вес машин в тоннах.

Количество осей	Одиночные автомобили, т	Автопоезда прицепные или седельные, т
Две	18	–
Три	25	28
Четыре	32	36
Пять	35	40
Шесть и более	–	44

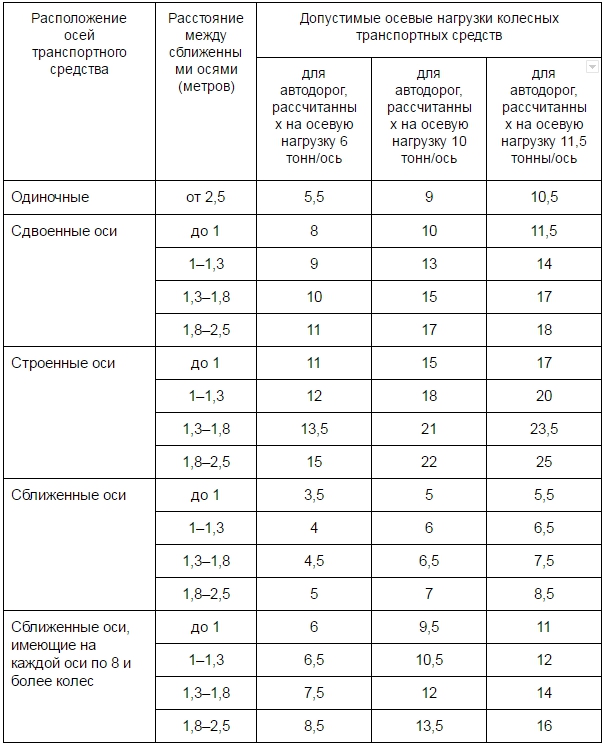
Вторая характеристика, устанавливаемый этим нормативным актом, – допустимая нагрузка. Она определяется в зависимости от вида дорог, типа колёс и расстояния между сближенными осями.

Например, таблица максимально разрешённых нагрузок на оси грузовых автомобилей для односкатных колёс выглядит следующим образом.

Значения в таблице приводятся для каждой оси. Расчёт массы должен производиться как можно точнее, так как допустимая погрешность не более 5 %.

Как рассчитать нагрузку

Итак, ограничение по проезду существует по двум параметрам:

Рассчитаем вес авто. Существует соотношение для двухосного автомобиля (например, марки Газель):

Ма=Нп+Нз,
где, Ма – вес грузовика.
Нп – нагрузка на переднюю ось.
Нз – аналогичный параметр для задней оси.

Эта простая формула расчёта связывает нагрузку на оси грузового автомобиля и его массу.

Для автотранспорта с тремя осями, задний и средний мост которого объединён в тележку (пример – Камаз 53215), эта зависимость имеет следующий вид:

где, Нт – нагрузка на всю заднюю тележку.

Нагрузка для задней тележки и оси обычно больше. Так как именно там располагают перевозимые товары. А вес, давящий на переднюю ось, определяется только массой кабины и силового агрегата.

Узнать нагрузку, имея вес груза, машины и прицепа – сложнее. И это расчёт будет иметь очень приблизительный вид.

Берем в свидетельствах о регистрации массу авто (Ма) и прицепа (Мп). Для примера возьмем Ма=6 т, Мп= 11 т.

Узнаем фактический вес груза (Мг). Примем Мг= 19 т.

Самое распространённое соотношение нагрузок: 0,75 – на прицеп, 0, 25 – на тягач. Тогда нагрузка на прицеп: Нп=0,75*(Мп+Мг)=22,5.

Считается, что нагрузка распределена в прицепе равномерно. И нагрузка на одну ось (Но) равна Нп/количество осей =22,5/3=7,5 т на каждую ось.

Аналогично считаем нагрузку на оси машины. На них приходятся оставшиеся 0,25 веса. То есть (Мп+Мг)*0,25+Ма=(11+19)*0,25+6=13,5 т.

Нагрузка на задние оси автомобиля будет равно 0,75 от нагрузки на грузовик. То есть 13,5*0,75/2=5,06.

А нагрузка на переднюю ось – то, что осталось от общей нагрузки на авто. 13,5–5,06*2=3,37.

Итого получается следующая примерная картина распределения веса 3,37+5,06+5,06+7,5+7,5+7,5.

Реальные значения могут отличаться. Часто нагрузка на осях бывает неравномерной. Это обычно связано со следующими причинами:

Цены на карты для тахографов можно узнать здесь.

Неисправностью подвески полуприцепа.

Прогибанием прицепа под грузом.

Негоризонтальностью площадки полуприцепа.

Конструктивными особенностями подвески.

Как определить нагрузку на ось грузового автомобиля

Взвешивание – простой способ определения как общего веса, так и значения для каждой отдельной оси. Есть два метода:

Динамический. Для взвешивания грузовик со скоростью не более 5 км/ч проезжает по поосным автомобильным весам. Они зафиксируют вес каждой оси, а потом определят вес самой машины. Это достаточно простой и удобный способ, но его погрешность составляет от 0,5 до 3%. Что – как вы можете понять при границе превышения максимальной допустимой нагрузки на ось грузового автомобиля в 2% – слишком много.

Статический. Авто въезжает и останавливается на платформе весов, на которую установлены тензодатчики. Их применение позволяет добиться очень высокой точности взвешивания – 0,01%.

Также можно купить тягач, оснащённый системой мониторинга, и совместимый с ним прицеп. Это довольно удобный способ всегда быть в курсе уровня загруженности своей машины, но очень дорогой.

Можно вмонтировать манометры в магистраль пневморессоры, и следить за показаниями в процессе погрузочных работ. Чтобы не мучится с определением, какое значение шкалы манометра какому весу соответствует, можно установить специальные датчики. Но это требует не только затрат денег при покупке всех элементов системы, но и значительных усилий по её отладке.

Штрафы за перегруз

В основном об этом виде административного наказания беспокоятся водители грузовиков. Так как у легковых автомобилей есть ограничения только по количеству перевозимых пассажиров. Штраф за превышение нагрузки разделяются на три типа в зависимости от уровня ответственности лиц:

Для физических лиц 1,5–2 тыс. руб.

Для должностных – сумма уже выше,15 тыс. руб.

И ещё выше для юридических – 400 тыс. руб.

Оформить заказ на карту для тахографа.

Если при превышении более 2% нет разрешения на провоз, то также оформляется штраф. Да и когда вес груза не совпадает с тем, что написано в сопроводительных бумагах с физического лица могут взыскать сумму 5 тыс. рублей. Для компании размер взыскания больше минимум в 50 раз. Правда, без контрольного взвешивания выписать штраф инспектор не имеет права.

Источник

Методика расчета нагрузки на ось для грузовых автоперевозок

Тяга к знаниям — она как «старость», в самый неожиданный момент может настичь любого. Вот и мы, застигнутые врасплох, протянули ручки к знаниям. Хотя все «изучали» в школе физику, но по жизни простейшая задачка вызывает ступор. Наша цель — понять возможности перераспределения нагрузок на оси тягача и полуприцепа при изменении расположения груза в полуприцепе. И применение этого знания на практике.

Все уравнения, описывающие наши объекты, относятся к тем моментам, когда они либо находятся в состоянии покоя, либо двигаются равномерно и прямолинейно (с точки зрения классической механики эти состояния описываются одними и теми же уравнениями и, находясь внутри системы, невозможно понять, покоится ли она или двигается равномерно и прямолинейно). В эти моменты сумма всех сил, действующих на каждый из рассматриваемых объектов, равна нулю. А также сумма всех моментов сил, действующих на каждый из объектов, равна нулю.

Наша задача не привязана к какому-либо конкретному типу тягачей, полуприцепов и грузов. Поэтому все формулы будут предоставлены в общем виде. Однако, поскольку нашей целью не является получение абстрактных формул и решение систем уравнений, а мы хотим решить практические вопросы, то величины, которые могут быть измерены на практике, будут полагаться известными. Кроме того, мы будем рассматривать двуосный тягач и одноосный полуприцеп. В нулевом приближении при увеличении количества осей у тягача и/или полуприцепа нагрузка на каждую ось уменьшается пропорционально. Т.е. если мы получим, что нагрузка на одну ось составляет 10 тонн, то замена одной оси на 2 приведёт к тому, что нагрузка на каждую из осей будет составлять 5 тонн. Если практические измерения покажут неприменимость такого подхода, при котором нагрузка делится между осями поровну, то необходимо будет уточнить и дополнить модель.

Рассмотрение системы из 3-х объектов будем проводить последовательно, т.е. сначала рассмотрим один тягач, затем добавим к нему полуприцеп, после чего добавим груз и посмотрим, как можно оптимизировать нагрузку на оси тягача и полуприцепа, изменяя положение груза в полуприцепе.

1. Тягач

Любая задача в механике начинается с рисунка, на котором отмечены все важные в контексте задачи геометрические размеры; силы, действующие на объекты; а также указана система отсчета, в которой мы пишем все уравнения.

Рисунок 1.

Итак, условие, что сумма всех сил, действующих на тело равна нулю, приводит нас к уравнению:

Рассмотрим ось, проходящую через переднюю ось грузовика (и направленную, как мы договаривались ранее, перпендикулярно плоскости рисунка). Сумма всех моментов сил действующих на тело, равна $0$. Это следует из того, что раз грузовик находится в состоянии покоя (а он очевидно находится в состоянии покоя, см. также замечание относительно состояния покоя и равномерного прямолинейного движения во вступлении), то он не вращается вокруг любой выбранной оси. Значит он не вращается в том числе вокруг оси, проходящей через переднюю ось грузовика. Это даёт нам уравнение:

Как можно применить формулу (1.3) на практике?

Для этого рассмотрим тягач Mercedes Actros 1841.

Данные взяты не из бумажек, измерения проводились на реальном пункте взвешивания — на весах. В баке было 500 литров дизельного топлива.

Расстояние между осями нашего тягача Mercedes Actros 1841 — 3600 мм.

Чтобы корректно подставить эти значения в формулу (1.3) обсудим сначала вопрос о размерности физических величин.

Масса — скалярная величина, измеряется в килограммах. Сила — векторная величина, измеряется в Ньютонах.

Таким образом, мы видим, что сила однозначно связана с массой, и в принципе, нам всё равно, в чём измерять силу — в Ньютонах или в килограммах — это вопрос договорённости. Когда речь идёт о нагрузке, которую оказывает автомобиль на дорогу, общепринятой единицей измерения этой нагрузки являются килограммы. В формулу (1.3) входит отношение нагрузки на заднюю ось к весу тягача. Вес (по определению) это сила, с которой тело давит на горизонтальную опору или растягивает вертикальный подвес. Таким образом, вес — это сила. Но раз мы договорились о том, что все силы мы измеряем не в Ньютонах (как мы все привыкли со школы), а в килограммах, то и вес тягача мы выражаем в килограммах. Т.е. от веса переходим к массе.

Итак, давайте рассчитаем расстояние от передней оси тягача Mercedes Actros 1841 по формуле (1.3) с учётом рассуждений о единицах измерения:

Все рассуждения о нагрузке, которая измеряется в килограммах, будут применяться и в дальнейшем при практическом применении выведенных формул. См., например, вычисление центра тяжести полуприцепа по формуле (2.4).

2. Тягач с полуприцепом

Если к тягачу, рассмотренному ранее, присоединён полуприцеп без груза, то нагрузка на его оси изменяется.

Рисунок 2.

Рассмотрим рис.2. Мы можем записать по отдельности для тягача и полуприцепа оба условия равновесия. Необходимо отметить, что положение центра тяжести тягача, вычисленное согласно (1.3), не изменится после присоединения полуприцепа.

Что даёт нам уравнение (2.1) с практической точки зрения? Если мы, зная массу тягача, измерим нагрузку на его переднюю и заднюю оси при присоединении пустого полуприцепа, то используя уравнение (2.1) мы можем вычислить силу, с которой пустой полуприцеп «давит» на тягач:

Рассмотрим теперь полуприцеп.

Для того чтобы определить, где находится центр тяжести полуприцепа (это важно — мы ищем положение центра тяжести именно самого полуприцепа, а не системы «тягач+пустой полуприцеп»), запишем условие равенства моментов сил, действующих на полуприцеп, относительно оси, проходящей через заднюю ось полуприцепа:

Эта формула пригодится нам в дальнейшем при рассмотрении груза, находящегося в полуприцепе. Также мы можем вычислить нагрузку на ось полуприцепа (считаем что ось на полуприцепе одна) по следующей формуле:

Полуприцеп трёхосный, но в рамках оговоренной ранее методики мы считаем нагрузку на каждую ось одинаковой. Посмотрим, к каким результатам нас это приведёт. Рассчитаем по формуле (2.2) силу взаимодействия тягача и полуприцепа, сила с которой полуприцеп давит на «седло» тягача:

Подставим теперь полученную величину в формулы (2.4) и (2.5):

Если теперь мы хотим рассчитать нагрузку на каждую из осей, то общую нагрузку необходимо поделить на 3 (т.к. у полуприцепа 3 оси). Полученный результат можно показать при помощи следующей таблицы:

Отклонение расчёта от

реального значения, кг

11706,71760-53,321706,71800-93,331706,71560146,7Итого5120,051200

3. Тягач с полуприцепом и грузом

Перейдём теперь к рассмотрению общего случая, когда в полуприцепе находится груз. Теперь мы должны на основании рассчитанных ранее характеристик грузовика и полуприцепа выяснить, как будут распределяться нагрузки на оси при различном положении груза. При этом необходимо сделать следующую оговорку: мы будем предполагать, что рама полуприцепа является идеально жесткой, не деформируется при наличии груза и распределяет нагрузку равномерно на каждый метр своей длины. Т.е. истории, подобные той, что описана на сайте в разделе страшных рассказов, выходят за рамки текущей задачи.

Рисунок 3.

Итак, запишем условие равенства сил, и моментов сил, действующих на тягач:

Теперь запишем аналогичную пару уравнений для полуприцепа, при этом условие равенства моментов сил будем рассматривать относительно задней оси полуприцепа.

Итак, запишем условие равенства сил, и моментов сил, действующих на тягач:

$ <\large m^\cdot g \cdot a + m^\cdot g \cdot X_^— N \cdot L^= 0 >$

4. Что нужно для расчета нагрузок на оси грузового автопоезда

Итак, любая модель подразумевает в первую очередь набор исходных данных; переменную величину, изменяющееся значение которой влияет на результаты; алгоритм расчёта и результат.

Что нам необходимо в качестве исходных данных?

Нужно геометрическое описание тягача и полуприцепа:

$<\large L_T>$	— расстояние между осями тягача;
$<\large l_1>$	— расстояние от передней оси тягача до точки сцепки с полуприцепом;
$<\large L^>$	— расстояние от задней оси полуприцепа до места сцепки с тягачом.

Необходимо знать распределение нагрузки на оси тягача без полуприцепа:

$<\large N_<1<,>0>^>$ — нагрузка на переднюю ось тягача;

$<\large N_<2<,>0>^>$ — нагрузка на заднюю ось тягача.

Необходимо знать распределение нагрузки на оси тягача при присоединении полуприцепа без груза:

$<\large N_<1<,>1>^>$ — нагрузка на переднюю ось тягача;
$<\large N_<2<,1>>^>$ — нагрузка на заднюю ось тягача.

Если каждый груз представляет из себя коробку, внутри которой вес распределен равномерно, то центр тяжести находится на середине ширины коробки. В данном случае шириной мы называем геометрический размер стороны коробки, параллельный борту полуприцепа.

Поупражняйтесь в расчетах и распределении груза

Мы сделали калькулятор для расчета нагрузок на оси грузового автопоезда в составе седельного тягача и полуприцепа.

5. О распределении нагрузки на задние оси полуприцепа

Ранее было сделано предположение о том, что нагрузка на задние оси полуприцепа распределяется равномерно. Это предположение приводит к расхождению теоретических расчётов с экспериментальными результатами. Причём пренебречь этими расхождениями мы не можем, поскольку они превышают точность измерений на статических весах в пунктах весового контроля.
Для учёта неравномерной нагрузки можно применить несколько различных подходов:

Ослабление исходной модели.

Давайте проверим, к чему нас это предположение приведёт. Уравнения (4.1), (4.2) принимают вид:

Источник

Методика расчета нагрузки на ось для грузовых автоперевозок

Тяга к знаниям — она как «старость», в самый неожиданный момент может настичь любого. Вот и мы, застигнутые врасплох, протянули ручки к знаниям. Хотя все «изучали» в школе физику, но по жизни простейшая задачка вызывает ступор. Наша цель — понять возможности перераспределения нагрузок на оси тягача и полуприцепа при изменении расположения груза в полуприцепе. И применение этого знания на практике.

Все уравнения, описывающие наши объекты, относятся к тем моментам, когда они либо находятся в состоянии покоя, либо двигаются равномерно и прямолинейно (с точки зрения классической механики эти состояния описываются одними и теми же уравнениями и, находясь внутри системы, невозможно понять, покоится ли она или двигается равномерно и прямолинейно). В эти моменты сумма всех сил, действующих на каждый из рассматриваемых объектов, равна нулю. А также сумма всех моментов сил, действующих на каждый из объектов, равна нулю.

Наша задача не привязана к какому-либо конкретному типу тягачей, полуприцепов и грузов. Поэтому все формулы будут предоставлены в общем виде. Однако, поскольку нашей целью не является получение абстрактных формул и решение систем уравнений, а мы хотим решить практические вопросы, то величины, которые могут быть измерены на практике, будут полагаться известными. Кроме того, мы будем рассматривать двуосный тягач и одноосный полуприцеп. В нулевом приближении при увеличении количества осей у тягача и/или полуприцепа нагрузка на каждую ось уменьшается пропорционально. Т.е. если мы получим, что нагрузка на одну ось составляет 10 тонн, то замена одной оси на 2 приведёт к тому, что нагрузка на каждую из осей будет составлять 5 тонн. Если практические измерения покажут неприменимость такого подхода, при котором нагрузка делится между осями поровну, то необходимо будет уточнить и дополнить модель.

Рассмотрение системы из 3-х объектов будем проводить последовательно, т.е. сначала рассмотрим один тягач, затем добавим к нему полуприцеп, после чего добавим груз и посмотрим, как можно оптимизировать нагрузку на оси тягача и полуприцепа, изменяя положение груза в полуприцепе.

1. Тягач

Любая задача в механике начинается с рисунка, на котором отмечены все важные в контексте задачи геометрические размеры; силы, действующие на объекты; а также указана система отсчета, в которой мы пишем все уравнения.

Рисунок 1.

Итак, условие, что сумма всех сил, действующих на тело равна нулю, приводит нас к уравнению:

Рассмотрим ось, проходящую через переднюю ось грузовика (и направленную, как мы договаривались ранее, перпендикулярно плоскости рисунка). Сумма всех моментов сил действующих на тело, равна $0$. Это следует из того, что раз грузовик находится в состоянии покоя (а он очевидно находится в состоянии покоя, см. также замечание относительно состояния покоя и равномерного прямолинейного движения во вступлении), то он не вращается вокруг любой выбранной оси. Значит он не вращается в том числе вокруг оси, проходящей через переднюю ось грузовика. Это даёт нам уравнение:

Как можно применить формулу (1.3) на практике?

Для этого рассмотрим тягач Mercedes Actros 1841.

Данные взяты не из бумажек, измерения проводились на реальном пункте взвешивания — на весах. В баке было 500 литров дизельного топлива.

Расстояние между осями нашего тягача Mercedes Actros 1841 — 3600 мм.

Чтобы корректно подставить эти значения в формулу (1.3) обсудим сначала вопрос о размерности физических величин.

Масса — скалярная величина, измеряется в килограммах. Сила — векторная величина, измеряется в Ньютонах.

Таким образом, мы видим, что сила однозначно связана с массой, и в принципе, нам всё равно, в чём измерять силу — в Ньютонах или в килограммах — это вопрос договорённости. Когда речь идёт о нагрузке, которую оказывает автомобиль на дорогу, общепринятой единицей измерения этой нагрузки являются килограммы. В формулу (1.3) входит отношение нагрузки на заднюю ось к весу тягача. Вес (по определению) это сила, с которой тело давит на горизонтальную опору или растягивает вертикальный подвес. Таким образом, вес — это сила. Но раз мы договорились о том, что все силы мы измеряем не в Ньютонах (как мы все привыкли со школы), а в килограммах, то и вес тягача мы выражаем в килограммах. Т.е. от веса переходим к массе.

Итак, давайте рассчитаем расстояние от передней оси тягача Mercedes Actros 1841 по формуле (1.3) с учётом рассуждений о единицах измерения:

Все рассуждения о нагрузке, которая измеряется в килограммах, будут применяться и в дальнейшем при практическом применении выведенных формул. См., например, вычисление центра тяжести полуприцепа по формуле (2.4).

2. Тягач с полуприцепом

Если к тягачу, рассмотренному ранее, присоединён полуприцеп без груза, то нагрузка на его оси изменяется.

Рисунок 2.

Рассмотрим рис.2. Мы можем записать по отдельности для тягача и полуприцепа оба условия равновесия. Необходимо отметить, что положение центра тяжести тягача, вычисленное согласно (1.3), не изменится после присоединения полуприцепа.

Что даёт нам уравнение (2.1) с практической точки зрения? Если мы, зная массу тягача, измерим нагрузку на его переднюю и заднюю оси при присоединении пустого полуприцепа, то используя уравнение (2.1) мы можем вычислить силу, с которой пустой полуприцеп «давит» на тягач:

Рассмотрим теперь полуприцеп.

Для того чтобы определить, где находится центр тяжести полуприцепа (это важно — мы ищем положение центра тяжести именно самого полуприцепа, а не системы «тягач+пустой полуприцеп»), запишем условие равенства моментов сил, действующих на полуприцеп, относительно оси, проходящей через заднюю ось полуприцепа:

Эта формула пригодится нам в дальнейшем при рассмотрении груза, находящегося в полуприцепе. Также мы можем вычислить нагрузку на ось полуприцепа (считаем что ось на полуприцепе одна) по следующей формуле:

Полуприцеп трёхосный, но в рамках оговоренной ранее методики мы считаем нагрузку на каждую ось одинаковой. Посмотрим, к каким результатам нас это приведёт. Рассчитаем по формуле (2.2) силу взаимодействия тягача и полуприцепа, сила с которой полуприцеп давит на «седло» тягача:

Подставим теперь полученную величину в формулы (2.4) и (2.5):

Если теперь мы хотим рассчитать нагрузку на каждую из осей, то общую нагрузку необходимо поделить на 3 (т.к. у полуприцепа 3 оси). Полученный результат можно показать при помощи следующей таблицы:

Отклонение расчёта от

реального значения, кг

11706,71760-53,321706,71800-93,331706,71560146,7Итого5120,051200

3. Тягач с полуприцепом и грузом

Перейдём теперь к рассмотрению общего случая, когда в полуприцепе находится груз. Теперь мы должны на основании рассчитанных ранее характеристик грузовика и полуприцепа выяснить, как будут распределяться нагрузки на оси при различном положении груза. При этом необходимо сделать следующую оговорку: мы будем предполагать, что рама полуприцепа является идеально жесткой, не деформируется при наличии груза и распределяет нагрузку равномерно на каждый метр своей длины. Т.е. истории, подобные той, что описана на сайте в разделе страшных рассказов, выходят за рамки текущей задачи.

Рисунок 3.

Итак, запишем условие равенства сил, и моментов сил, действующих на тягач:

Теперь запишем аналогичную пару уравнений для полуприцепа, при этом условие равенства моментов сил будем рассматривать относительно задней оси полуприцепа.

Итак, запишем условие равенства сил, и моментов сил, действующих на тягач:

$ <\large m^\cdot g \cdot a + m^\cdot g \cdot X_^— N \cdot L^= 0 >$

4. Что нужно для расчета нагрузок на оси грузового автопоезда

Итак, любая модель подразумевает в первую очередь набор исходных данных; переменную величину, изменяющееся значение которой влияет на результаты; алгоритм расчёта и результат.

Что нам необходимо в качестве исходных данных?

Нужно геометрическое описание тягача и полуприцепа:

$<\large L_T>$	— расстояние между осями тягача;
$<\large l_1>$	— расстояние от передней оси тягача до точки сцепки с полуприцепом;
$<\large L^>$	— расстояние от задней оси полуприцепа до места сцепки с тягачом.

Необходимо знать распределение нагрузки на оси тягача без полуприцепа:

$<\large N_<1<,>0>^>$ — нагрузка на переднюю ось тягача;

$<\large N_<2<,>0>^>$ — нагрузка на заднюю ось тягача.

Необходимо знать распределение нагрузки на оси тягача при присоединении полуприцепа без груза:

$<\large N_<1<,>1>^>$ — нагрузка на переднюю ось тягача;
$<\large N_<2<,1>>^>$ — нагрузка на заднюю ось тягача.

Если каждый груз представляет из себя коробку, внутри которой вес распределен равномерно, то центр тяжести находится на середине ширины коробки. В данном случае шириной мы называем геометрический размер стороны коробки, параллельный борту полуприцепа.

Поупражняйтесь в расчетах и распределении груза

Мы сделали калькулятор для расчета нагрузок на оси грузового автопоезда в составе седельного тягача и полуприцепа.

5. О распределении нагрузки на задние оси полуприцепа

Ранее было сделано предположение о том, что нагрузка на задние оси полуприцепа распределяется равномерно. Это предположение приводит к расхождению теоретических расчётов с экспериментальными результатами. Причём пренебречь этими расхождениями мы не можем, поскольку они превышают точность измерений на статических весах в пунктах весового контроля.
Для учёта неравномерной нагрузки можно применить несколько различных подходов:

Ослабление исходной модели.

Давайте проверим, к чему нас это предположение приведёт. Уравнения (4.1), (4.2) принимают вид:

Источник