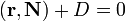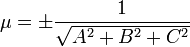Плоскость что это такое в геометрии

Плоскость (математика)

Плоскость (математика)

Пло́скость — одно из основных понятий геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. Уравнение плоскости впервые встречается у А. К. Клеро (1731), уравнение плоскости в отрезках, по-видимому, впервые встречается у Г.Ламе (1816—1818), нормальное уравнение ввёл Л. О. Гессе (1861).

Содержание

Некоторые характеристические свойства плоскости

Аналогично отрезку и интервалу, плоскость не включающую крайние точки можно назвать интервальной плоскостью или открытой плоскостью.

Уравнения плоскоcти

Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.

где A,B,C и D — постоянные, причём A,B и C одновременно не равны нулю; в векторной форме:

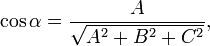
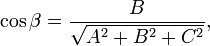
(смешанное произведение векторов), иначе

где 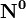— единичный вектор, p — расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель

(знаки μ и D противоположны).

Расстояние от точки до плоскости

Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.

Расстояние между параллельными плоскостями

Связанные понятия

Если в векторной форме, то

где α и β — любые числа, не равные одновременно нулю.

Плоскости в четырёхмерном пространстве

Если в четырёхмерном пространстве две плоскости лежат в одной гиперплоскости, то они могут либо быть параллельными (в частности, совпадать), либо пересекаться по линии.

Если же две плоскости не лежат в одной гиперплоскости, то они либо не пересекаются (скрещиваются, подобно тому как в трёхмерном пространстве скрещиваются прямые), либо имеют ровно одну общую точку.

Пересечение двух плоскостей в точке (а не по линии, как в трёхмерном пространстве) можно проиллюстрировать следующим примером. Пусть дана система декартовых координат x y z t. Пусть две плоскости α и β проходят через начало координат, причём плоскость α содержит координатные прямые x и y, а плоскость β содержит координатные прямые z и t. Соответственно у всех точек плоскости α координаты z и t равны 0, а у всех точек плоскости β координаты x и y равны 0. Тогда очевидно, что единственная точка, которая может принадлежать обеим плоскостям — это точка (0,0,0,0).

Литература

Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: ФИЗМАТЛИТ, 2002. — 240 с.

Источник

Плоскость (геометрия)

Плоскость — одно из основных понятий геометрии. Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, проходящие через какие-либо две точки плоскости. В алгебре плоскость определяется как двухмерное аффинное пространство.

В планиметрии плоскость рассматривается как универсуум, к которому принадлежат все геометрические фигуры. Стереометрия рассматривает бесконечное множество плоскостей, принадлежащих к пространству.

[править] Некоторые характерные свойства плоскости

[править] Уравнения плоскости

Впервые встречается у А. К. Клеро (1731).

Уравнение плоскости в отрезках, по-видимому, впервые встречается у Г. Ламе (1816—1818).

Нормальное уравнение ввёл Л. О. Гессе (1861).

Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.

где [math]A,B,C[/math] и [math]D[/math] — постоянные, причём [math]A,B[/math] и [math]C[/math] одновременно не равны нулю; в векторной форме:

(смешанное произведение векторов), иначе

(знаки [math]\mu[/math] и [math]D[/math] противоположны).

Источник

Лекция 3. Плоскость

3.1. Способы задания плоскости на ортогональных чертежах

Рисунок 3.1 – Способы задания плоскостей

Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.

Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

Плоскость общего положения может иметь три следа: горизонтальный – απ₁, фронтальный – απ₂ и профильный – απ₃, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π₁, фронтальной π₂ и профильной π₃ (Рисунок 3.2).

Рисунок 3.2 – Следы плоскости общего положения

3.2. Плоскости частного положения

Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС

Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).

Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.

Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 – Эпюры плоскостей частного положения

3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).

Рисунок 3.5 – Принадлежность точки плоскости

Рисунок 3.6 – Принадлежность прямой плоскости

\left.\begin\alpha=m\parallel n,\\D\in\alpha\\C\in\alpha\\\end\right\> \Longrightarrow CD\in\alpha

Упражнение

Рисунок 3.7 – Решение задачи

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π₁) (Рисунок 3.8, а; 3.9).

Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π₂) (Рисунок 3.8, б; 3.10).

Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π₃) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).

\alpha=m\cap n\\\left.\begina_2\parallel m_2\\a_1\parallel m_1\\\end\right\> \Rightarrow a\parallel\alpha

Рисунок 3.12 – Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:

Рисунок 3.13 – Построение точки встречи прямой с плоскостью

Упражнение

Заданы: прямая АВ общего положения, плоскость σ⊥π₁. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.

Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).

Требуется построить точку пересечения прямой EF с плоскостью σ.

Рисунок 3.15 – Пересечение прямой с плоскостью

3.6. Определение видимости методом конкурирующих точек

При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π₁ или π₂.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π₂ (рис. 3.15)
Выберем точки, конкурирующие на π₂ – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π₂ надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π₂.
Направление взгляда на π₂ показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π₂, видно, что точка 4₁ располагается ближе к наблюдателю, чем 3₁.
4₁∈E₁F₁ ⇒ 4∈EF ⇒ на π₂ будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π₁.
Для определения видимости выберем точки, конкурирующие на π₁ – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π₁ надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π₁.
Направление взгляда на π₁ показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π₁, видно, что точка 2₂ располагается ближе к наблюдателю, чем 5₂.
2₂∈А₂В₂ ⇒ 2∈АВ ⇒ на π₁ будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.16 – Задание прямой, перпендикулярной плоскости

Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)

Теорема доказывается через теорему о проецировании прямого угла в частном случае.

Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).

Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.

3.8. Взаимное положение двух плоскостей

3.8.1. Параллельность плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Упражнение

Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).

Через точку F провести плоскость β, параллельную плоскости α.

Рисунок 3.17 – Построение плоскости, параллельной заданной

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Упражнение

Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами

Упражнение

Алгоритм решения задачи :

\left.\beginAB\cap\sigma=K\\AC\cap\sigma=L\\\end\right\> \left.\begin\Rightarrow A_1B_1\cap\sigma_1=K_1 \rightarrow K_2\\\Rightarrow A_1C_1\cap \sigma_1=L_1 \rightarrow L_2\\\end\right.

KL – линия пересечения ΔАВС и σ (α∩σ = KL).

Рисунок 3.19 – Пересечение плоскостей общего и частного положения

Упражнение

Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)

Алгоритм решения задачи :

\left.\begin\alpha\cap\sigma=(4-5)\\\beta\cap\sigma=(3-2)\\\end\right\>\\\left.\begin\alpha\cap\tau=(6-7)\\\beta\cap\tau=(1-8)\\\end\right\>\left.\begin(4_1-5_1)\cap(3_1-2_1)=M_1\rightarrow M_2\\(6_1-7_1)\cap(1_1-8_1)=N_1\rightarrow N_2\\\end\right\>\rightarrow\\\left.\beginM_1N_1\\M_2N_2\\\end\right\>\Rightarrow\alpha\cap\beta=MN

Упражнение

Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).

Рисунок 3.21 Решение задачи на пересечение плоскостей

Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π₂, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π₂ (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.

3.8.3. Взаимно перпендикулярные плоскости

Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Упражнение

Задана плоскость σ⊥π₂ и прямая общего положения – DE (Рисунок 3.22)

Требуется построить через DE плоскость τ⊥σ.

Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C₁D₁ должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение

Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС

3.9. Задачи для самостоятельного решения

1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.

Постройте фронтальную проекцию точки К.

2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).

3. Постройте проекции квадрата, принадлежащего плоскости α⊥π₂, если его диагональ MN //π₂ (Рисунок 3.26).

4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).

5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.

6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π₁.

7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π₁.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №3. Введение в стереометрию

Перечень вопросов, рассматриваемых в теме

Геометрия— это наука о свойствах геометрических фигур.

Планиметрия— это раздел геометрии, в котором изучаются свойства фигур на плоскости.

Стереометрия— это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Простейшими (основными) фигурами в пространстве являются точки, прямые и плоскости.

Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии. 10 кл. Москва.: Просвещение, 2013 г. С. 1-4

Зив Б. Г. Геометрия. 10 класс. Дидактические материалы.: Москва, Просвещение, 2013 г. С.4, 14, 24

Открытый электронный ресурс:

Решу ЕГЭ. Открытый образовательный портал. https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Мы закончили изучать и повторять раздел геометрии, который называется планиметрией.

В планиметрии все фигуры, которые рассматривались при доказательстве каждой теоремы или при решении задач, располагались на плоскости. Таким образом, мы имели дело только с одной плоскостью.

Сегодня мы начинаем изучать новый раздел геометрии, который называется стереометрией.

Обратите внимание на данные фигуры. Как вы заметили- они объемные.

И их все объединяет раздел геометрии Стереометрия.

Что же такое стереометрия?

По аналогии с планиметрией мы можем вывести следующее определение:

Стереометрия- это раздел геометрии, в котором изучаются свойства фигур в пространстве.

Простейшими (основными) фигурами в пространстве являются точки, прямые и плоскости.

Вместе с этими фигурами рассматриваются геометрические тела и их поверхности. Представления о геометрических телах дают нам: кристаллы (составлен из многоугольников) – многогранники; куб; капли жидкости в невесомости – шар; футбольный мяч (шар); консервная банка (цилиндр).

Изучая свойства геометрических фигур, мы получаем представления о геометрических свойствах реальных предметов. В этом и состоит практическое значение геометрии, в частности стереометрия, широко используется в строительстве, архитектуре, машиностроении, геодезии, в науке и технике.

В планиметрии основными фигурами были точки и прямые. В стереометрии наряду с ними рассматривается ещё одна основная фигура – плоскость.

Представление плоскости нам дает любая гладкая поверхность. Она безгранична.

Основные свойства точек, прямых и плоскостей, касающиеся их взаимного расположения, выражены в аксиомах.

А1: Через 3 точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Точки А α, В α, С α.

Если взять четыре произвольные точки, то через них может не проходить ни одна плоскость.

А2: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

В этом случае говорят, что прямая лежит в плоскости или плоскость проходит через прямую.

Это свойство используется при проверке “ровности” линейки.

Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.

А3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

В этом случае говорят, что плоскости пересекаются по прямой.

Пример: пересечение пола и стены

В пространстве существует бесконечно много плоскостей, и в каждой плоскости справедливы все аксиомы и теоремы планиметрии.

Некоторые следствия из аксиом.

Теорема 1: Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Дано: а – прямая, точка М ∉ а.

Доказать: 1) существует α: а α.

1) Дополнительные построения: т. В а, т. С а.

2) В, С, М не лежат на одной прямой, следовательно, по первой аксиоме существует плоскость α.

4) Единственность α. следует из того, что любая плоскость, проходящая через прямую а и т. М, проходит через М, В, С. Значит, она совпадает с α (по Аксиоме 1). Теорема доказана.

Теорема 2: Через две пересекающиеся прямые проходит плоскость, и, причём только одна.

Дано: а ∩ b в точке М

Доказать: существование плоскости α, а α, b α.

1) Дополнительные построения: N Є b, N∉ a.

2) Существует α : N α, a α.

3)

4) Из 2) и 3) следует α. проходит через прямые а и b.

5) Единственность α следует из того, что любая плоскость, проходящая через прямые а и b, проходит через точку N, значит она совпадает с α (по Теореме 1). Теорема доказана.

Разбор решения заданий тренировочного модуля

Тип задания: выделение цветом

Прямая MN пересекает плоскость:

Внимательно рассмотрите рисунок, как вы видите прямая MN пересекает плоскости ABC и A₁B₁С_1, рассмотрим варианты ответов, среди них есть вариант 2) (ABC), он и является верным.

Тип задания: смежный граф

Пользуясь данным рисунком

назовите три плоскости, содержащие прямую DС₁ (нижний индекс записываете цифрой после буквы, без пробела)

Решение: Внимательно рассмотрите прилагающийся рисунок, определите, где на нем располагается прямая DС₁, как вы видите из рисунка он располагается в плоскостях:

Источник