Плоскость поделена на области несколькими прямыми докажите что эти области
Плоскость поделена на области несколькими прямыми докажите что эти области
Задача 1: Из квадрата клетчатой бумаги размером 2 n × 2 n вырезали одну клетку. Докажите, что полученную фигуру можно разрезать на «уголки» из трёх клеток (
).
Решение: Указание: Переход: разбиваем квадрат на четыре квадрата 2 n – 1 × 2 n – 1 и вырезаем из каждой недырявой части угловую клетку так, чтобы вырезанные клетки образовали уголок.
Задача 2: Докажите, что любую сумму, начиная с 8 тугриков, можно выплатить купюрами по 3 тугрика и 5 тугриков.
Решение: Указание: Переход: меняем купюру в 5 тугриков на две купюры по 3 тугрика. Если же пятитугриковых купюр нет – меняем три купюры по 3 тугрика на две купюры по 5 тугриков…
Задача 3: Приведите пример натурального числа, которое равно сумме а) трёх своих различных делителей; б) ста своих различных делителей.
Решение: а) 6; б) 2 97 6. Переход: n → 2n (в список суммируемых делителей добавляется число n).
Задача 4: Докажите, что при каждом натуральном n, начиная с 3, существует выпуклый n-угольник, имеющий ровно три острых угла.
Решение: Указание: Переход: стороны AB и BC, образуюшие тупой угол, заменяем на отрезок A′C′ (A′ ∈ AB; C′ ∈ BC). Вновь образованные углы AA′C′ и CC′A – внешние углы треугольника A′BC′, а значит «тупее» угла B…
Задача 5: У бородатого многоугольника во внешнюю сторону растет щетина. Его пересекает несколько прямых общего положения, на каждой из которых с одной из сторон растут волосы. В результате многоугольник оказался разбитым на некоторое число частей. Докажите, что хотя бы одна из частей окажется волосатой снаружи.
Решение: Указание: Проводим прямые одну за другой. Если очередная прямая пересекает волосатую снаружи часть, то часть, оказавшаяся с неволосатой стороны – также волосатая снаружи…
Задача 6: [Игра «Ханойская башня»] Имеется пирамида с n кольцами возрастающих размеров (внизу – самое большое) и еще два пустых стержня той же высоты. Разрешается перекладывать верхнее кольцо с одного стержня на другой, но при этом запрещается класть большее кольцо на меньшее. Докажите, что
а) можно переложить все кольца с первого стержня на один из пустых стержней;
б) это можно сделать не более, чем за 2 n – 1 перекладываний.
Решение: Указание: Пусть мы умеем переность пирамиду высоты k – 1.
1. Перенести k – 1 кольцо на пустой стержень
2. Перенести k-е кольцо на другой пустой стержень.
3. Переносим k – 1 кольцо на тот же стержень
Задача 7: Плоскость поделена на области несколькими прямыми. Докажите, что эти области можно раскрасить в два цвета так, чтобы любые две соседние области были раскрашены в различные цвета. (Соседними считаются области, имеющие общий участок границы.)
Задача 8: В прямоугольнике 3 × n (3 строки, n столбцов) расставлены фишки трёх цветов по n штук каждого цвета. Докажите, что переставляя фишки в строчках, можно сделать так, чтобы в каждом столбце были фишки всех трёх цветов.
Задача 9: Плоскость поделена на области несколькими прямыми и окружностями. Докажите, что эти области можно раскрасить в два цвета так, чтобы любые две соседние области были раскрашены в различные цвета. (Соседними считаются области, имеющие общий участок границы.)
Плоскость поделена на области несколькими прямыми докажите что эти области
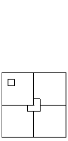
Несколько прямых делят плоскость на части. Докажите, что эти части можно раскрасить в 2 цвета так, что граничащие части будут иметь разный цвет.
Подсказка
Рассуждайте, используя индукцию по количеству прямых.
Решение
Будем использовать индукцию по количеству прямых n. При n = 1 утверждение задачи очевидно: достаточно покрасить две полуплоскости, на которые одна прямая делит плоскость, в разные цвета. Пусть утверждение задачи верно для k прямых. Рассмотрим некоторые k + 1 прямых. «Забывая» пока про (k+1)-ю прямую, раскрасим области, на которые делят плоскость остальные k прямых, в два цвета так, что граничащие части будут иметь разный цвет (это можно сделать по предположению индукции). При такой раскраске области, граничащие по (k+1)-й прямой, будут иметь одинаковый цвет. Далее перекрасим все области, расположенные по одну из сторон относительно (k+1)-й прямой, в противоположный цвет. Полученная в результате раскраска удовлетворяет условию задачи.
Источники и прецеденты использования
| книга | |
| Автор | Алфутова Н.Б., Устинов А.В. |
| Год издания | 2002 |
| Название | Алгебра и теория чисел |
| Издательство | МЦНМО |
| Издание | 1 |
| глава | |
| Номер | 1 |
| Название | Метод математической индукции |
| Тема | Индукция |
| параграф | |
| Номер | 3 |
| Название | Индукция в геометрии и комбинаторике |
| Тема | Индукция (прочее) |
| задача | |
| Номер | 01.054 |
| web-сайт | |
| задача | |
Плоскость поделена на области несколькими прямыми докажите что эти области
Задача 1: Из квадрата клетчатой бумаги размером 2 n × 2 n вырезали одну клетку. Докажите, что полученную фигуру можно разрезать на «уголки» из трёх клеток ().
Задача 2: Докажите, что любую сумму, начиная с 8 тугриков, можно выплатить купюрами по 3 тугрика и 5 тугриков.
Задача 3: Приведите пример натурального числа, которое равно сумме а) трёх своих различных делителей; б) ста своих различных делителей.
Задача 4: Докажите, что при каждом натуральном n, начиная с 3, существует выпуклый n-угольник, имеющий ровно три острых угла.
Задача 5: У бородатого многоугольника во внешнюю сторону растет щетина. Его пересекает несколько прямых общего положения, на каждой из которых с одной из сторон растут волосы. В результате многоугольник оказался разбитым на некоторое число частей. Докажите, что хотя бы одна из частей окажется волосатой снаружи.
Задача 6: [Игра «Ханойская башня»] Имеется пирамида с n кольцами возрастающих размеров (внизу – самое большое) и еще два пустых стержня той же высоты. Разрешается перекладывать верхнее кольцо с одного стержня на другой, но при этом запрещается класть большее кольцо на меньшее. Докажите, что
а) можно переложить все кольца с первого стержня на один из пустых стержней;
б) это можно сделать не более, чем за 2 n – 1 перекладываний.
Задача 7: Плоскость поделена на области несколькими прямыми. Докажите, что эти области можно раскрасить в два цвета так, чтобы любые две соседние области были раскрашены в различные цвета. (Соседними считаются области, имеющие общий участок границы.)
Задача 8: В прямоугольнике 3 × n (3 строки, n столбцов) расставлены фишки трёх цветов по n штук каждого цвета. Докажите, что переставляя фишки в строчках, можно сделать так, чтобы в каждом столбце были фишки всех трёх цветов.
Задача 9: Плоскость поделена на области несколькими прямыми и окружностями. Докажите, что эти области можно раскрасить в два цвета так, чтобы любые две соседние области были раскрашены в различные цвета. (Соседними считаются области, имеющие общий участок границы.)
Геометрия. 10 класс
Параллельность плоскостей
Параллельность плоскостей
Необходимо запомнить
Определение. Плоскости, которые не пересекаются, называются параллельными.
Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Свойства параллельных плоскостей.
Теорема 1. Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны.
Теорема 2. Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.
Теорема 3. Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.
Теорема 4. Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость.
Теорема 5. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.
Параллельность плоскостей
Разберём и докажем теорему.
Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.
Пусть нам даны плоскость α и точка М, ей не принадлежащая.
Докажем, что существует плоскость β, которой принадлежит точка М, параллельная плоскости α.
В данной плоскости α проведём две произвольные пересекающиеся прямые a и b. Через точку M проведём прямые a1 и b1, параллельные соответственно a и b. Плоскость, проходящую через пересекающиеся прямые a1 и b1, обозначим β. На основании признака параллельности плоскостей плоскость β параллельна плоскости α.
Докажем методом от противного, что β – единственная плоскость, удовлетворяющая условию теоремы.
Допустим, что через точку M проходит другая плоскость, например β1, параллельная α.
Так как β1 пересекает плоскость β (они имеют общую точку M), то по теореме 4 плоскость β1 пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку M можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β – единственна. Теорема доказана.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №6. Параллельность плоскостей
Перечень вопросов, рассматриваемых в теме
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии 10 Москва «Просвещение» 2013 год. С. 1-4.
Зив Б. Г. Геометрия 10 класс Дидактические материалы Москва «Просвещение» 2013 год. С.4, 14, 24
Теоретический материал для самостоятельного изучения
Как известно из аксиом стереометрии, если плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Значит две плоскости или пересекаются, или не пересекаются.
Определение. Плоскости, которые не пересекаются, называются параллельными.
Параллельные плоскости α и β обозначаются α∥β.
Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны.
Допустим, что плоскости α и β не параллельны, то есть они пересекаются по некоторой прямой c.
Прямая a1 параллельна прямой b1, значит она параллельна и самой плоскости β.
Прямая a2 параллельна прямой b2, значит она параллельна и самой плоскости β (признак параллельности прямой и плоскости).
Прямая c принадлежит плоскости α, значит хотя бы одна из прямых a1 или a2 пересекает прямую c, то есть имеет с ней общую точку. Но прямая c также принадлежит и плоскости β, значит, пересекая прямую c, прямая a1 или a2 пересекает плоскость β, чего быть не может, так как прямые a1 и a2 параллельны плоскости β.
Из этого следует, что плоскости α и β не пересекаются, то есть они параллельны.
Свойства параллельных плоскостей.
Теорема 1. Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны.
Плоскость α пересекается с плоскостью γ по прямой a.
Плоскость β пересекается с плоскостью γ по прямой b.
Линии пересечения a и b лежат в одной плоскости γ и потому могут быть либо пересекающимися, либо параллельными прямыми. Но, принадлежа двум параллельным плоскостям, они не могут иметь общих точек. Следовательно, они параллельны.
Теорема 2. Отрезки параллельных прямых, заключенных между двумя параллельными плоскостями, равны.
Проведённая плоскость пересекается с плоскостью α по прямой AB, а с плоскостью β по прямой CD.
По предыдущей теореме прямые AB и CD параллельны. Четырехугольник ABCD есть параллелограмм (у него противоположные стороны параллельны). А раз это параллелограмм, то противоположные стороны у него равны, то есть BC=AD.
Теорема 3. Если прямая пересекает одну из двух параллельных плоскостей, то она пересекает и другую.
Пусть α||β, a пересекает α в точке А.
Выберем в плоскости любую точку C. Через эту точку и прямую a проведём плоскость.
Так как плоскость имеет с плоскостями α и β общие точки A и C соответственно, то она пересекает эти плоскости по некоторым прямым b и c, которые проходят соответственно через точки A и C. По предыдущей теореме прямые b и c параллельны. Тогда в плоскости прямая a пересекает (в точке A) прямую b, которая параллельна прямой c. Значит, прямая a пересекает и прямую c в некоторой точке B. Так как прямая c лежит в плоскости, то точка B является точкой пересечения прямой a и плоскости. Теорема доказана.
Теорема 4. Если плоскость пересекает одну из двух параллельных плоскостей, то она пересекает и другую плоскость.
Пусть α||β, α и γ пересекаются.
Докажем, что плоскости β и γ пересекаются.
Проведём в плоскости γ прямую a, пересекающую плоскость α в некоторой точке B. Тогда по теореме 3 прямая a пересекает и плоскость β в некоторой точке A. Следовательно, плоскости β и γ имеют общую точку A, т. е. пересекаются. Теорема доказана.
Теорема 5. Через точку, не лежащую в данной плоскости, можно провести плоскость, параллельную данной, и притом только одну.
Пусть нам даны плоскость α и точка М, ей не принадлежащая.
Докажем, что существует плоскость β, которой принадлежит точка М, параллельная плоскости α.
В данной плоскости α проведём две произвольные пересекающиеся прямые a и b. Через точку M проведём прямые a1 и b1, параллельные соответственно a и b. Плоскость, проходящую через пересекающиеся прямые a1 и b1, обозначим β. На основании признака параллельности плоскостей плоскость β параллельна плоскости α.
Докажем методом от противного, что β — единственная плоскость, удовлетворяющая условию теоремы.
Допустим, что через точку M проходит другая плоскость, например β1, параллельная α.
Так как β1 пересекает плоскость β (они имеют общую точку M), то по теореме 4 плоскость β1 пересекает и плоскость α (β ‖ α). Мы пришли к противоречию. Таким образом, предположение о том, что через точку M можно провести плоскость, отличную от плоскости β и параллельную плоскости α, неверно. Значит, плоскость β — единственна. Теорема доказана.
Рассмотрим несколько примеров на применение данных свойств.
Даны две пересекающиеся прямые a и b точка А, не лежащая в плоскости этих прямых. Докажите, что через точку А проходит плоскость, параллельная прямым a и b, и притом только одна.
Прямые a и b пересекаются по условию, следовательно, по следствию из аксиомы А1, эти прямые единственным образом определяют плоскость α.
Известно, что через точку А, не принадлежащую плоскости α, проходит единственная плоскость, параллельная α, т.е. параллельная прямым a и b (по теореме 5) .
Плоскости α и β параллельны, прямая m лежит в плоскости α. Докажите, что прямая m параллельна плоскости β.
Предположим, что прямая m пересекает плоскость β в точке М. Тогда точка М принадлежит плоскости α (т.к. прямая m лежит в плоскости α) и М принадлежит плоскости β, значит, α и β пересекаются, но они параллельны по условию. Очевидно, m не пересекает плоскость α, т.е. параллельна ей.
Примеры и разбор решения заданий тренировочного модуля
№1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Три отрезка А1А2, В1В2 и С1С2, не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости А1В1С1 и А2В2С2 параллельны.
Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2 параллельны.
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
Рассмотрим плоскость, проходящую через прямые А1А2 и В1В2
(она существует и единственная, т.к. прямые пересекаются).
В этой плоскости лежит четырехугольник А1В1А2В2, диагонали которого точкой пересечения делятся пополам. Следовательно, данный четырехугольник является параллелограммом (признак параллелограмма), значит, А1В1 и А2В2 параллельны.
Аналогично доказывается параллельность В1С1 и В2С2. Из вышеперечисленного следует, что плоскости А1В1С1 и А2В2С2 параллельны по признаку параллельности плоскостей.
Тип задания: выделение цветом
Два равнобедренных треугольника FKС и FKD с общим основанием FK расположены так, что точка С не лежит в плоскости FKD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам KС и KD.
Прямые, которые содержат медианы треугольников к KC и KD- выходят из одной точки F. Соответственно, можно сделать вывод, что данные прямые пересекаются.