Требуемая доходность акции формула
Как рассчитать дивидендную и полную доходность акции: формулы и коэффициенты
Инвестпривет, друзья! Доходность акций на фондовом рынке формируется за счет двух составляющих. Первая – это рост курсовой стоимости ценной бумаги. Вторая – дивиденды. Если у компании всё хорошо, то ее финансовые показатели повышаются, дивиденды увеличиваются и, как следствие, курс акций тоже растет. Давайте разбираться, чем виды доходности акций отличаются друг от друга, как их рассчитывать и как платить налоги.
Доходность акций на фондовом рынке
Итак, инвестор получает доход с акций двумя способами: за счет роста стоимости акции и за счет получаемых дивидендов.
В конце 19 – начале 20 века основным доходом на фондовой бирже считались дивиденды. Инвесторы скупали акции как раз для получения стабильного денежного потока. Компании стремились нарастить дивидендные выплаты, и именно их размер считался основной «пузомеркой» акционерного общества.
Однако после Великой Депрессии ситуация изменилась. Многие компании отказались от практики выплаты дивидендов. Вместо этого они сфокусировались на удержании прибыли внутри компании (а дивиденды – это как раз часть прибыли) и реинвестировании своих доходов в собственный бизнес.
За счет реинвеста прибыли росли показатели компании – в результате акции дорожали. Сейчас рост курсовой стоимости акции считается основным доходом инвестора на бирже, а дивиденды – приятным дополнением к общей прибыли.
Есть компании, которые вообще не выплачивают дивиденды, но которые очень хорошо растут. Хрестоматийные примеры – акции Google (Alphabet), Facebook, Tesla, Berkshire Hathaway, в России – Яндекс, Лента, Русал, М.Видео. В основном – это активно развивающиеся компании, которые вкладывают свои деньги в собственное развитие, новые разработки, покупку стартапов и т.д. Словом, руководству есть куда потратить прибыль, чем просто распределять ее между акционерами.
Но это свойственно только для зрелых рынков (типа США, Британии, Германии, Японии). На развивающихся рынках (например, России, Индии и Китая) дивидендная доходность акции продолжает играть главенствующую роль при определении котировок. Если компания не платит дивиденды, сокращает их или меняет политику выплат, то ее котировки падают. Если выплаты увеличиваются – котировки растут. Это одна из ключевых особенностей фондового рынка России.
Следовательно, на развивающихся рынках цена и доходность акций связаны и зависят друг от друга. Чем выше ожидаемая доходность акции, тем дороже стоит ценная бумага. Компании, которые на российском фондовом рынке стабильно платят дивиденды, увеличивая их размер, дорожают. Их немного, но они есть, например, Лукойл, Сбербанк, Татнефть.
Средняя доходность акций на разных рынках, понятное дело, будет разной. В США, например, дивидендная доходность акций в среднем равна 2-3% годовых. В тоже время в России этот показатель равен 7-9% годовых, и это один из самых больших показателей в мире.
Среднюю доходность акций конкретного рынка можно оценить, исходя их роста индекса. На сколько вырос индекс, на столько в среднем по больнице выросли акции. Но это очень грубая оценка. Если индекс вырос на 40%, это не говорит, что все акции в нем возросли на это значение. Какие-то акции могут вырасти на 60%, какие-то – всего на 10%, а какие-то и вовсе могут упасть.
Поэтому нет понятия «средняя доходность акций» – в каждом случае нужно смотреть индивидуально.
Таким образом, итоговая доходность акций складывается их двух составляющих:
Доходность выражается в процентах или номинальном значении. Например, если акция стоила 200 рублей, а через год – 224 рубля, то говорят, что ее доходность составила 12% годовых или 24 рубля за год.
В ходе инвестирования можно получить и отрицательную доходность, если курсовая стоимость акции в итоге оказалась меньше начальной. Даже наличие дивидендов не всегда нивелирует убыток.
Например, акция на момент покупки стоила 850 рублей, на момент продажи – 600, были получены дивиденды в размере 50 рублей. В итоге доходность составит –18,75%.
Дивидендная доходность
Компания может платить дивиденды раз в год, полгода, квартал или даже ежемесячно. Решение о выплате дивидендов принимает Совет директоров, а утверждает их собрание акционеров. Чтобы получить дивиденды, нужно владеть акциями на день отсечки – т.е. последний день, когда они выплачиваются.
Дивидендная доходность акций определяется как отношение размера перечисленного дивиденда к курсу акции на конкретную дату. Есть несколько дат, относительно которых рассчитывают дивиденды (т.е. в этот день смотрят на цену акции):
Иногда высчитывают средневзвешенную цену акции в течение года и высчитывают дивидендную доходность относительно этого значения – но это путь извращенцев 🙂
Понятно, что значение дивдоходности – динамическое. Размер объявленных дивидендов остается таким же, но котировки самой акции меняются буквально ежесекундно.
Поэтому дивидендная доходность меняется каждый день, и если вы где-то вычитали о высокой дивдоходности акции – перепроверьте данные. Возможно, цена уже «подтянулась», и ваша сделка окажется не такой выгодной.
По умолчанию дивидендная доходность рассчитывается как отношение размера дивиденда к курсу акций на дату отсечки. Если вы видите в каком-нибудь аналитическом материале дивидендный доход по акции – то расчет, скорее всего, делался на дату отсечки.
Формула расчета дивдоходности акции такова:
Например, за 2018 год Газпром выплатил 16,61 рублей на акцию. Дата отсечки – 18.07.2019. В тот день акции стоили 238,01 рубль. Дивидендная доходность – 6,97%.
Как я писал выше, дивиденды бывают годовые, полугодовые, квартальные (промежуточные) или ежемесячные. Если компания платит дивиденды за квартал, то рассчитываемая дивидендная доходность тоже будет квартальной. Чтобы рассчитать годовую дивидендную доходность, нужно сложить все дивиденды за год и разделить их на цену акции в день последней выплаты.
Как я уже писал, дивидендная доходность российских акций составляет в среднем от 7% до 12% годовых.
Рыночная доходность акций
Доходность, получившаяся за счет роста курсовой стоимости, рассчитывается по такой формуле:
Интерактив. Отличие требуемой доходности от E/P
Добрый день! Меня зовут Андрей Валухов.
В комментариях к статье Коэффициент P/BV (P/B) Андрей спрашивает:
Андрей дополнительно отмечает: «фактически вы оцениваете положение компании относительно рынка (отрасли), используя лишь параметры самой компании (P, E, Bv) и не используя параметров рынка (отрасли).
Представьте: мой рост 180 см, вес 75 кг. Можно ли на основании этого сделать выводы о моей физической форме относительно жителей моего многоэтажного дома, не используя грубых допущений?»
Андрей! Спасибо за Ваш вопрос.
Во-первых, следует остановиться на том, как мы применяем равенство ROE/R и P/BV. Данная формула является краеугольным камнем нашей системы расчета потенциальной доходности долевых инструментов. Используя собственные прогнозы операционных и финансовых результатов той или иной компании, а также величины собственного капитала, мы оцениваем линейку ROE компании, как правило, на 5-6 лет вперед. Далее мы соотносим стабильное значение ROE с требуемой доходностью от вложения в акции – R. Полученное значение ROE/R является ориентиром для мультипликатора P/BV, с помощью которого, зная показатель BV в будущем, можно определить справедливую, на наш взгляд, цену акции. Соответственно, высокая потенциальная доходность возникает из разницы текущей и справедливой цены.
Далее отдельно остановимся на R. R – это требуемая доходность от вложения в акции компании. Мы рассчитываем ее для каждой компании отдельно, и ее значение состоит из нескольких слагаемых. Проиллюстрируем это на примере Новатэка.
Согласно последнему обновлению осенью 2015 года, базовая ставка по Новатэку составляла 12%. В тот период второй выпуск биржевых облигаций компании с погашением в октябре 2015 года торговался с доходностью 10.9%. Поскольку доходность коротких облигаций в данном случае не является репрезентативной, мы экспертно оценили базовую ставку компании на уровне 12%, что ниже среднеотраслевого значения для нефтегазовых компаний первого эшелона на уровне 12.2%.
Таким образом, R или требуемая доходность от вложения в акции Новатэка составит 13.3%. И существенную часть в итоговой оценке занимает базовая ставка по эмитенту, на которую влияет уровень процентных ставок в экономике. Поэтому Ваши тезисы о том, что R не имеет никакого отношения к депозитам, а также то, что мы оцениваем компании, используя лишь параметры самих эмитентов, не верны.
Далее перейдем к рассмотрению случая переоцененности. Действительно, когда акции какой-либо компании оценены высоко, то ее E/P может быть низок. Однако ROE/R и E/P нельзя рассматривать как взаимосвязанные величины! Первый параметр определяется исключительно финансовыми результатами компании и уровнем процентных ставок, в то время как второй – может быть подвержен значительным колебаниям из-за курсовой динамики акций. Таким образом, E/P – это ставка доходности, которую инвестор будет получать в виде чистой прибыли, если купит акции компании сейчас. Если он будет экстремально высок, то это найдет свое отражение, как Вы правильно замечаете, в текущем высоком значении мультипликатора P/BV, снижая тем самым потенциальную доходность акций такой компании.
Еще раз отметим, не следует путать E/P складывающийся из соотношения фактических цены и прибыли с требуемой доходностью R, используемой для вычисления потенциальной доходности акций.
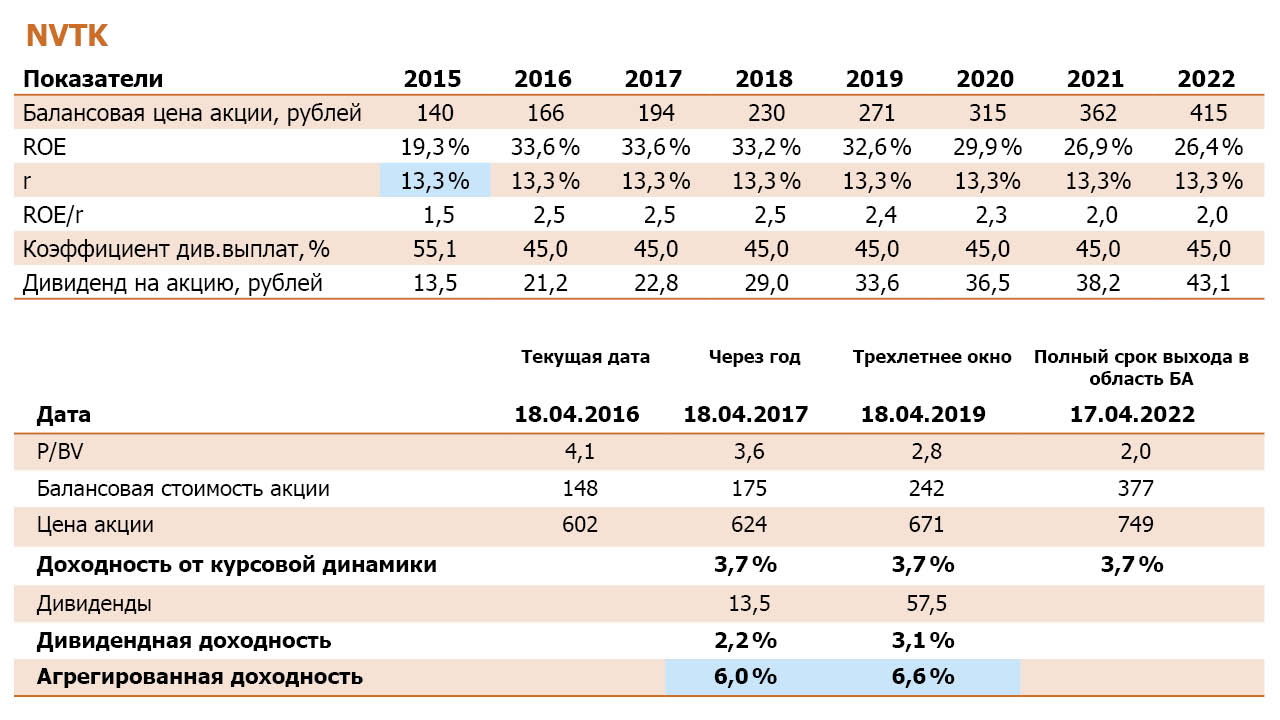
Для демонстрации переоцененности обратимся к примеру того же Новатэка.
Как видно из наших расчетов, срок достижения Новатэком справедливого значения по Мультипликатору P/BV – 6 лет. По итогам 2022 года ROE компании составит 26.4%, что почти вдвое будет превышать требуемую ставку доходности, а значит P/BV, по нашим оценкам, в это время должен составить 1.98. Исходя из прогнозного значения балансовой цены акции около 380 рублей нетрудно рассчитать справедливую цену 748 рублей, что выливается в доходность от курсовой динамики в 24% за шесть лет или 3.7% в год.
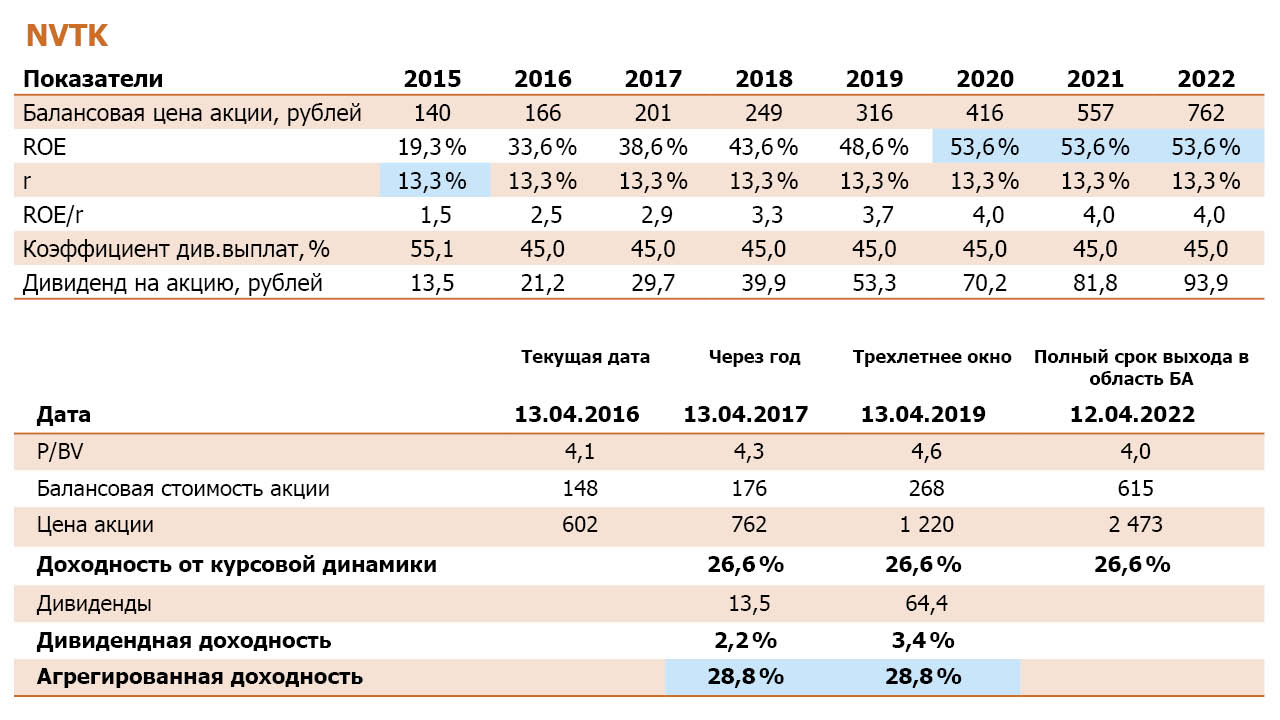
Гипотетически эта компания обладала бы неплохой потенциальной доходностью, если бы смогла бы демонстрировать стабильный ROE к 2022 году на уровне 54%.
Надеемся, что полно и понятно ответили на Ваши вопросы и замечания.
Требуемая доходность | Required Rate of Return
Требуемая доходность или требуемая ставка доходности (англ. Required Rate of Return) является одним из ключевых показателей, который широко используется в инвестиционной сфере и корпоративных финансах. В общем виде эту экономическую категорию можно определить как минимальную процентную ставку, под которую инвестор будет согласен осуществить вложение своих средств. Чтобы определить ее, необходимо принять во внимание безрисковую процентную ставку, доходность рыночного портфеля, риск инфляции, риск ликвидности и прочие факторы. В корпоративных финансах требуемая ставка доходности используется для оценки инвестиционных проектов и анализа дисконтированных денежных потоков. Поскольку этот показатель используется в разных сферах, методика его расчета и использования имеет существенные различия, которые следует рассмотреть более подробно.
Модель оценки капитальных активов CAPM
Одним методов оценки требуемой ставки доходности при осуществлении инвестиций в акции является модель оценки капитальных активов (англ. Capital Asset Price Model, CAPM), которая выглядит следующим образом:
где ki – требуемая ставка доходности для i-ой акции;
KRF – безрисковая процентная ставка;

(Подробнее о модели CAPM можно прочитать здесь)
Подход на основе дисконтирования дивидендов
Оценка требуемой доходности акций также может производиться на основе концепции дисконтирования денежных потоков, которые возникают в результате выплаты дивидендов. В общем виде модель постоянного роста дивидендов можно представить следующим образом:
где P0 – текущая рыночная цена акции;
D1 – ожидаемый размер дивиденда;
ke – требуемая ставка доходности;
g – темп прироста дивидендов.
Таким образом, формула расчета требуемой ставки доходности будет выглядеть так:
(Подробнее о модели постоянного роста дивидендов можно прочитать здесь)
Требуемая доходность в корпоративных финансах
Практическое применение такого показателя как требуемая доходность распространяется не только на оценку инвестиционных решений о вложении средств в акции. Корпорации постоянно сталкиваются с необходимостью оценки различных инвестиционных проектов, не связанных с вложениями в ценные бумаги, например, расширение производственных возможностей, выход на новые рынки сбыта или запуск новых видов продукции. В этом случае требуемая ставка доходности для реализации такого проекта будет равна средневзвешенной стоимости капитала корпорации (англ. Weighted Average Cost of Capital, WACC).
Формула расчета этого показателя выглядит следующим образом:
где wd – удельный вес заемного капитала;
kd – стоимость заемного капитала;
kce – стоимость обыкновенного акционерного капитала;
kpe – стоимость привилегированного акционерного капитала;
T – ставка корпоративного налога на прибыль.
Дисконтирование денежных потоков
Помимо всего вышеперечисленного, требуемая ставка доходности также нашла широкое применение и в других моделях, основывающихся на принципе дисконтирования денежных потоков, в частности для:
Выводы
Методика оценки требуемой ставки доходности является достаточно сложной в практическом применении, поскольку может основываться на различных методических подходах. Также процесс ее оценки затруднен тем, что аналитику необходимо учитывать большое количество прочих факторов, таких как инфляция, ликвидность, деловая активность и т.д., которые влияют на рыночную стоимость активов. Однако правильная оценка требуемой доходности позволит выбрать правильные инвестиционные решения.
Как посчитать доходность акции: виды доходности и их расчет
Для чего нужно знать доходность?
Сравнивать доходность следует грамотно. Если проводить сравнение по суммам дивидендов за 1 акцию, результат будет некорректным.
Расчеты доходности помогут выбрать ценные бумаги, определить справедливую стоимость. Для прогнозирования эффективности инвестиций нужно учитывать дополнительно стоимость фактической продажи актива.
Размер дивидендов зависит от кредитных ограничений. Некоторые кредиторы запрещают компании повышать их уровень и даже выплачивать дивиденды. Благоприятным фактором для владельцев американских акций становится требование налоговиков о запрете накопления чрезмерной прибыли. Если налоговая служба определит доход компании как избыточную прибыль, она будет облагаться налогом по завышенной ставке 39,6 %. Поэтому в США компании предпочитают регулярно выплачивать дивиденды.
Примеры расчета доходности
Дивидендная доходность иностранных активов ниже по сравнению с российскими. Для Америки 3–5 % считается высоким уровнем. Низкие показатели связаны с низкой ставкой Федерального резерва, но в качестве компенсации риски снижены до умеренных. Высокодоходные активы США традиционно считают высокорисковыми.
Основываясь на годовых выплатах за последний отчетный период, можно спрогнозировать будущие дивиденды. Но оценка будет неточной. Эксперты дают дивидендным инвесторам рекомендации:
Дивидендная доходность представляет собой часть прибыли, которой компания делится с акционерами. Дивиденды выплачиваются раз в квартал, полугодие или год. Сумма обсуждается на собрании акционеров.
Дивидендная
Рассчитывается, как отношение размера дивидендов к стоимости 1 акции. Формула выглядит следующим образом: r = d / p * 100, где буквой d обозначается сумма дивидендов, а буквой p актуальная цена акции.
Пример: совет директоров установил по итогам года дивиденд в 10 рублей. Стоимость акции на Московской бирже 150 рублей. Округленная сумма дивидендной доходности 6,67 %.
Дивиденды выплачиваются раз в год, в квартал или полгода, иногда раз в месяц. Если дивиденды выплачиваются раз в полгода, то и доходность будет полугодовой. Чтобы посчитать доходность за год, нужно суммировать все выплаты за 12 месяцев и разделить на стоимость акции на день последних выплат.
Текущая (рыночная)
Пример: если купить бумаги по 150 рублей, а по мере роста котировок продать по 190 рублей за штуку, текущая доходность получится 26,67 %.
Полная
Годовая
Служит для оценки привлекательности ценных бумаг, поскольку часто котировки и финансовые результаты недостаточно точно отражают реальную ситуацию. Владелец актива может держать его меньше и больше года. Для сравнения доходности акций и депозитов необходимо равнозначное значение. Им становится доходность в годовых процентах. Для вычисления доходность умножают на коэффициент k = 365 / число дней реального обладания акциями.
Конечная
Сначала рассчитывается стоимость покупки и продажи:
Рр = 100 руб. × 1,7 = 170 руб.
Ps = 170 руб. × 1,25 = 212,5 руб.
Далее определяется текущая доходность:
Дивиденды в первый год 15 руб., текущая доходность во второй – 20 %. Получается 170 руб. × 0,2 = 34 руб.
Учитывая ставку 45 % в течение третьего года, получение дивидендов только за 3 квартала, получается доходность за третий год равна 100 руб. × 0,45 × 0,75 = 37,5 руб.
Расчет среднегодового дивиденда: (15 + 34 + 37,5) : 2,75 = 31,45 руб.
Если подставить все величины в формулу, получится конечная доходность:
(31,45 + 42,5 / 2,75) / 170 × 100 % = 26,79 %.
Получается, что на каждый рубль, который инвестор вложил в покупку акции, среднегодовой доход составил около 27 коп. без учета налогов.
На доходность акций влияют разные факторы, многие из которых не поддаются прогнозу:
Перечисленные в статье базовые формулы помогут самостоятельно посчитать доходность акций. Крупные компании на своих сайтах предлагают отчеты в открытом доступе. Используя эти цифры и размер дивидендов, можно быстро определить стоимость бумаг. Полагаться лишь на котировки биржи мало, следует прогнозировать риски на базе точных цифр.
Подпишитесь на нашу рассылку, и каждое утро в вашем почтовом ящике будет актуальная информация по всем рынкам.
Как считать индикаторы инвестиционной привлекательности активов
На примере портфеля Уоррена Баффетта
Практически всегда действует правило: чем выше возможная доходность, тем выше риски.
Но вот в обратную сторону правило работает не всегда, и это обидно: потенциальная доходность по активу так себе, а риск этого актива довольно высокий. Получается, для относительно невысокой доходности приходится рисковать так, будто вкладываешься в высокодоходный актив. В этом случае на помощь инвестору может прийти расчет соотношения «риск-доходность».
В статье я рассмотрю показатели, по которым можно оценить, насколько адекватно у определенного актива соотношение его риска и доходности. Вот какие показатели буду рассматривать:
Но прежде чем разбираться с показателями риска-доходности, нужно разобраться и с основой — с тем, как считаются сами доходность и риск.
Как считается доходность
Доходность — это показатель, характеризующий финансовый результат от инвестирования. Простыми словами, это процент от стоимости актива, который инвестор заработал «сверху». В общем виде доходность от вложения в финансовый актив считается так:
где Pt + 1 — цена актива сейчас или на момент продажи,
Pt — цена актива на момент покупки,
CF — промежуточный денежный поток, который принес актив за время владения им, — например, выплаченные дивиденды.
(150 − 100 + 3) / 100 = 0,53, или 53%
Для упрощения расчетов из формулы иногда убирают CF — промежуточные денежные потоки в виде дивидендов.
В зависимости от того, за какой период мы рассчитываем доходность, она может быть дневной, месячной, квартальной, годовой или общей.
(115,6 − 27,4) / 27,4 = 3,22, или 322%
Но доходность за все время владения инструментом не так показательна, если мы хотим сравнить активы, которыми владели в течение разных периодов. Например, один актив принес вам 11% за полгода, а второй — 30% за полтора года. Чтобы сравнить эффективность этих инструментов, их доходности нужно привести к общему знаменателю — годовой доходности. Годовая доходность показывает, сколько в среднем приносил актив за год владения им.
Для расчета годовой доходности можно использовать три подхода — в зависимости от того, какими данными владеет инвестор. Если есть сразу все данные, можно использовать любой из способов — результат будет одинаковый.
Если есть информация о доходности за каждый год владения активом, то доходность рассчитывается по следующей формуле:
где rn — доходность за каждый анализируемый период,
n — количество периодов (лет).
((1 + 20%) × (1 − 10%) × (1 + 30%)) 1/3 − 1 = 11,98%
Кажется, что формула слишком сложная и что можно было бы просто взять доходность за каждый год, сложить и поделить на три — то есть посчитать среднее арифметическое. Но корректнее считать не среднее арифметическое, а среднее геометрическое — что и делает наша формула. И этому есть причина.
Для примера выше среднее арифметическое составило бы 13,33%:
Наше значение, полученное через среднее геометрическое, на 1,35 процентного пункта меньше. Геометрический показатель учитывает, что доходность неравномерна и меняется от года к году, — то есть такая доходность уже учитывает в себе некоторую волатильность.
Другими словами, чем выше волатильность актива, тем ниже будет значение среднего геометрического доходности к среднему арифметическому.
Для примера возьмем акции A и B и предположим, что за 4 года после покупки акции показали одинаковую итоговую доходность. Но на протяжении этих четырех лет вели себя по-разному : акции A росли более плавно, а акции B сильнее проседали и сильнее росли, то есть были более волатильными.
Котировки акций A и B за 4 года
Посчитаем данные для обоих активов: среднее арифметическое и среднее геометрическое, то есть годовую доходность.
Среднее арифметическое: (40% + 7% − 17% + 44%) / 4 = 18,5%.
Среднее геометрическое (годовая доходность): (1 + 40%) × (1 + 7%) × (1 − 17%) × (1 + 44%) 1/4 = 15,8%.
Среднее арифметическое: (−30% + 71% − 17% + 80%) = 26%.
Среднее геометрическое (годовая доходность): (1 − 30%) × (1 + 71%) × (1 − 17%) × (1 + 80%) 1/4 = 15,8%.
Среднее арифметическое актива А больше, чем актива В, — и если бы мы посчитали только среднее арифметическое, то сделали бы ложный вывод, что акции актива B выгоднее. Но ведь мы знаем, что это не так: в результате акции принесли одинаковую прибыль.
Годовая доходность по обеим акциям одинаковая — 15,8%. Но у акций B больше волатильность — и это выражается в разнице между средним арифметическим и средним геометрическим: чем она больше, тем больше волатильность.
В случае с акцией A разница между двумя арифметическим и геометрическим равна 2,8 процентных пункта. А у акции B эта разница составляет 10,4 процентных пункта — при равных доходностях по этой разнице можно сделать вывод, что акции B более волатильны.
Если известна совокупная доходность за весь срок владения, то формула для расчета годовой доходности будет выглядеть так:
(1 + Общая доходность) (365 / Количество дней владения активом) − 1
(1 + 74%) (365 / 715) − 1 = 32,68%
Таким образом, на инвестициях в компанию инвестор заработал 32,68% годовых за рассматриваемый период.
Если известна начальная и конечная стоимость инвестиций, то общую годовую доходность можно вычислить по следующей формуле:
(Конечная стоимость актива / Начальная стоимость актива) (1 / Количество периодов) − 1
((270 × 20 + 2 × 20) / 200 × 20) (1/2) − 1 = 16,62%
Совокупная доходность в данном кейсе составила 36%, а общая годовая доходность — 16,62%.
Как победить выгорание
Как считается риск
Риск — это вероятность частичной или полной потери вложенного капитала. В классической портфельной теории риск вложения определяется как стандартное отклонение его доходности — то есть возможный разброс его фактической доходности вокруг средней доходности.
Предположим, в среднем акция растет на 10% в год, но при этом возможны отклонения на 5% в каждую сторону — то есть она может вырасти как на 15% в год, так и на 5%. Вот эти возможные отклонения нам и нужно рассчитать. Рассчитывается стандартное отклонение по следующей формуле:
где rn — доходность за n-й период, обычно годовая,
r̄ — среднее арифметическое доходности актива за все время владения,
n — количество периодов: если считаем по годовой доходности, то количество лет.
Например, инвестор владел активом 4 года — он знает доходность за каждый год и теперь хочет рассчитать стандартное отклонение доходности этого актива.
Доходность актива
| Период | Доходность |
|---|---|
| Первый год | −11,5% |
| Второй год | 15,9% |
| Третий год | 10% |
| Четвертый год | 7,2% |
Чтобы посчитать стандартное отклонение доходности, в первую очередь посчитаем — среднее арифметическое доходности:
(−11,5% + 15,9% + 10% + 7,2%) / 4 = 5,4%
Теперь можем подставить данные в формулу выше:
Стандартное отклонение составило 11,8%. Если допустить, что доходность акции нормально распределена, то по правилу трех сигм инвестор вправе ожидать, что с вероятностью 68,3% (одно стандартное отклонение — 68,3% вероятности) доходность акции в следующем году будет находиться в диапазоне от −6,4% до 17,2% — то есть от (5,4% − 11,8%) до (5,4% + 11,8%).
Правило трех сигм гласит, что практически все значения нормально распределенной случайной величины лежат в диапазоне трех стандартных отклонений от среднего арифметического значения случайной величины. Случайной величиной у нас выступает годовая доходность по акции
Чем сильнее значения фактической доходности отклоняются от ее среднего значения, тем больше стандартное отклонение, а значит, больше риск. Низкое значение стандартного отклонения означает, что годовые доходности лежат вблизи среднего значения и риск от вложения в актив невелик.
Формулу выше используют в случаях, если берутся котировки по акции не за весь период ее существования, а, предположим, за 2—3 года из возможных 10 лет, прошедших с момента первичного размещения акции на фондовом рынке. А если берутся котировки за весь период существования акции, то для расчета стандартного отклонения используется следующая формула — она отличается только знаменателем — берется полное количество периодов:
Анализируем на примере портфеля Баффетта
Для примера возьмем портфель Уоррена Баффетта: я взял те активы, по которым есть данные котировок за период с 2012 по 2020 год. По отчетным данным на 30 сентября 2020 года в портфель Баффетта входило 49 компаний, но лишь по 6 компаниям, составляющим существенную долю портфеля, были данные за нужный период.