Что такое равносильный переход

Что такое равносильный переход

В нашем задании большую роль будет играть понятие равносильности.

называются равносильными на множестве `X`, если каждое решение первого неравенства (уравнения), принадлежащее множеству `X`, является решением второго и, наоборот, каждое решение второго, принадлежащее `X`, является решением первого, или, если, ни одно из неравенств (уравнений) на `X` не имеет решений. Т. е. два неравенства (уравнения) равносильны, по определению, если множества решений этих неравенств (уравнений) на `X` совпадают.

Отсюда следует, что вместо того, чтобы решать данное неравенство (уравнение), можно решать любое другое, равносильное данному. Замену одного неравенства (уравнения) другим, равносильным данному на `X`, называют равносильным переходом на `X`. Равносильный переход обозначают двойной стрелкой `hArr`. Если уравнение `f(x) = 0` (или неравенство) `f(x) > 0`) равносильно уравнению `g(x) = 0` (или неравенству `g(x) > 0`), то это мы будем обозначать так:

`f(x) = 0 hArr g(x) = 0` (или `f(x) > 0 hArr g(x) > 0`).

При каких значениях параметра `a` системы

Решим сначала первую, более простую систему

Подставим `a = 3` во вторую систему

Следовательно, при `a = 3` системы равносильны, т. к. при этом значении параметра обе системы не имеют решений.

Итак, таких `a` три: `0, 1, 2`. Но при этих `a` вторая система может иметь и другие решения, а если у неё других решений нет, то её единственное решение может не совпадать с решением первой системы, и тогда такое `a` не удовлетворяет условию задачи. Проверим эти значения параметра.

2. `a=1`: Вторая система имеет вид

Следовательно, системы не равносильны, т. к. вторая имеет два решения.

Следовательно, системы при этом значении `a` равносильны – они имеют единственное решение `(4; 0)`.

Источник

40. Алгебра Читать 0 мин.

40.710. Равносильные системы

Два неравенства являются равносильными, если множества их решений совпадают. При решении неравенств иногда приходится переходить от одного неравенства к другому, более простому. Рассмотрим несколько равносильных переходов: для решения иррациональных, показательных, логарифмических неравенств, неравенств с модулем, дробно-рациональных неравенств.

1. Равносильные переходы для решения иррациональных неравенств

Для избавления от радикалов в иррациональных неравенствах требуется умение возводить обе части неравенства в соответствующую степень. Однако нужно быть осторожными при возведении в четную степень, если хотя бы одна из частей неравенства отрицательная. Неосторожное возведение в квадрат неравенства может повлечь за собой приобретение или потерю решений.

Пример. Решите неравенство

Решение. Применим равносильный переход:

Встречаются такие неравенства, в которых корень сравнивают с выражением. Тогда тоже пользуемся возведением в квадрат для избавления от иррациональности, однако, накладываем дополнительное ограничение – неотрицательность выражения, поскольку значение корня четной степени – число неотрицательное.

Пример. Решите неравенство

Воспользуемся равносильным переходом.

Решение. Воспользуемся равносильным переходом:

Если неизвестная входит как в основание, так и в показатель степени, то заранее неизвестно, будет ли основание степени больше или меньше единицы, поэтому при решении неравенства нужно учитывать оба этих случая. Если неравенство строгое, то получаем следующий равносильный переход:

$(\phi (x))^ &gt (\phi (x))^\Leftrightarrow \left[ \begin \left\< \begin f(x)>g(x) \\ \phi (x) &gt 1 \end \right. \\ \left\< \begin f(x) &lt g(x) \\ 0 &lt \phi (x) (x+5)^<4>$

Используем следующий равносильный переход:

Если неравенство нестрогое, то нужно дополнительно рассмотреть случай – основание равно единице, т.к. тогда получается, что единица в любой степени равна единице, неравенство выполнится. Т.е. получаем следующий равносильный переход:

Используем следующий равносильный переход:

3. Равносильные переходы для решения логарифмических неравенств

Метод решений простейших логарифмических неравенств опирается на монотонность логарифмической функции, т.е. на правило отбрасывания логарифмов. Однако есть отличие от аналогичного правила отбрасывания оснований, которое объясняется тем, что при отбрасывании логарифмов расширяется ОДЗ неравенства. Значит, выражения, стоящие под логарифмами после отбрасывания последних могут стать отрицательными или равными нулю, следовательно, мы должны дополнительно учесть, что подлогарифмическое выражение положительно.

Если неизвестная входит как в основание, так и под знак логарифма, то заранее неизвестно, будет ли основание больше или меньше единицы, поэтому при решении неравенства нужно учитывать оба этих случая.

Воспользуемся равносильным переходом:

Решением первой системы является интервал (0;0,5)

При решении неравенств второй системы видим, что пересечений решений нет.

Таким образом, решением совокупности является интервал (0;0,5)

Пример. Решите неравенство

Воспользуемся равносильным переходом:

При нанесении решений каждого неравенства системы на числовую прямую видим, что пересечений решений нет. Значит, неравенство не имеет решений.

4. Равносильные переходы для решения неравенств, содержащих знак модуля

Если модуль меньше функции, то избавляемся от модуля, но взамен получаем систему из двух неравенств. Учитываем случаи: если число под модулем положительно и если число под модулем отрицательно:

Решение. Воспользуемся равносильным переходом:

Рассмотренный пример наглядно демонстрирует, что метод работает всегда. Мы помним, что модуль числа по определению является величиной неотрицательной. В примере модуль меньше отрицательного числа, очевидно, что такое неравенство не имеет решений.

Пример. Решите неравенство

$\left\vert x+4\right\vert &lt 2x$

Воспользуемся равносильным переходом.

Решением системы является луч (4;∞).

Пример. Решите неравенство

$\left\vert x+2\right\vert \leq 5x$

Воспользуемся равносильным переходом.

Решением системы является луч (0,5;∞).

Если модуль больше выражения, то здесь иной равносильный переход.

Другими словами, мы рассматриваем два случая: 1) сначала просто игнорируем модуль — решаем обычное неравенство; 2) затем по сути раскрываем модуль со знаком «минус», а затем умножаем обе части неравенства на −1, меня при этом знак. При этом варианты объединены квадратной скобкой, т.е. перед нами совокупность двух требований.

Пример. Решите неравенство

$\left\vert x-7\right\vert >8x$

Воспользуемся равносильным переходом.

Решением совокупности является луч (-∞;1).

Пример. Решите неравенство

$\left\vert 2x+8\right\vert \geq x-5$

Воспользуемся равносильным переходом.

Решением совокупности является луч все множество действительных значений

5. Метод расщепления неравенств

То есть иными словами, дробь положительна, когда числитель и знаменатель одного знака; дробь отрицательна, когда числитель и знаменатель разных знаков.

Произведение двух множителей равносильно совокупности систем:

То есть иными словами, произведение двух множителей положительно, когда оба множителя одного знака; произведение отрицательно, когда оба множителя разных знаков.

Решение. Воспользуемся равносильным переходом.

Решение первой системы – луч [15;∞)

Решение второй системы – открытый луч (-∞;4).

Решение. Воспользуемся равносильным переходом.

Решение первой системы – полуинтервал (1;1,5]

Вторая система не имеет решений.

Источник

Репетитор по математике о работе с равносильными переходами

Конечно, это разделение приблизительное. Уровень учеников бывают разным и проблемы одного слабого школьника могут принципиально отличаться от проблем другого. Поэтому репетитор по математике принимает решение о выборе методики в каждой конкретной ситуации, зависимо от способностей и знаний абитуриента.

Существует два принципиально разных подхода к обучению проводить равносильные преобразования: смысловой и механический. Какая бы подготовка к ЕГЭ по математике репетитором не проводилась, выделяются несколько видов простейших неравенств и уравнений со схемами и правилами, позволяющими заменить их равносильной совокупностью более простых объектов.

Они поясняются и заучиваются. Так чаще всего обучается средний ученик: репетитор по математике подробно объясняет причины включения в систему тех или иных объектов, а затем отрабатывает умение выявлять и использовать их в потоке задач.

Работа репетитора по математике с сильным учеником

Сильный ученик, как правило, получает необходимые навыки и без однообразных тренировок. Ему достаточно подбросить идею, объяснить принцип и показать один – два примера. Репетитор только направляет и контролирует ученика. Например, при решении неравенства log_<0,3>‘ style=’vertical-align:-30%’ alt=’log_<0,3>>log_<0,3>‘ />, понимая свойство монотонности логарифма, сильный школьник сам сможет составить систему, со всеми необходимыми проверками по ОДЗ и удалением из нее лишних неравенств – следствий:

В такой ситуации проводить отдельную работу по заучиванию базовыъ схем решений не требуется. Понять чем заменить логарифмическое неравенство вида сильный ученик сможет даже при переменном основании. Основные силы репетитор по математике бросает на отработку навыков перехода от первоначального неравенства к простейшему типу. Ситуации с потерей корней по причине сужения ОДЗ – наиболее типичная ошибка в этом случае. Именно ее провоцируют составители ЕГЭ по математике в задача C3 и репетитору крайне важно ее предупредить. Даже таллантливые дети иногда разкалывают логариф от произведения или сносят четный показатель под знаком логарифма в его коэффициент:

Стоит отдельно остановиться на применении логарифмических формул, меняющих ОДЗ. Важно показать пример и на потерю корня и на его приобретение. Я очень люблю использовать уравнение . Оно решается двумя способами: один с вынесением показателя в коэффициент перед логарифмом (при котором теряется корень х=-1), а другой напрямую, приравнивая подлогарифмические выражения друг к другу.

Все примеры, на которых репетитор по математике демонстрирует последствия неосмысленных преобразований должны быть простыми. Вопрос о потере и приобретении корней очень тонкий и требует предельной концентрации внимания ученика. Репетитор, нагружающий их многочисленными функциями и действиями, усложняет, таким образом, анализ ситуации. Задача преподавателя математики состоит не в том, чтобы дать в момент объяснений умственную нагрузку способному абитуриенту, а сфокуссировать внимание ученика на проблеме, сделать пример ярким и запоминающимся. Разница лишь в том, что сильному ученику достаточно одного единственного показа без многократного обращения к нему в течение всей подготовки к ЕГЭ.

Практика ведения преобразований в уравненях и неравенствах на пути получения их простейших видов — основное направление в работе репетитора с сильным учеником. Комбинации функций бывают самые разные. Больше всего неприятностей связано с ОДЗ. В случае сомнений в его сохранности лучше всего найти ОДЗ у каждого объекта и сравнить эти множества. Если они совпадают – переход равносильный (конечно если применялись формулы, а не возведение, например, в четную степень). Главное, чтобы область не сужалось. Если она расширилась, нужно добавить в новую систему условия выполнения ОДЗ от предыдущего уравнения (неравенства).

В работе с сильным учеником репетитор по математике может использовать метод точного объяснения равносильного перехода. В чем он заключается? Доказывается совпадение двух ответов систем на уровне множеств. Из верности условий в одной системе (при некотором значении переменной) должна вытекать верность условий в другой системе и наоборот. Если это доказано – переход равносильный.

Для запоминания опасных переходов, то я советую репетиторам оформлять формулы так:

Даже простое переворачивание логарифма при смене основания таит в себе опасность потерять или приобрести лишний корень (при котором f (x)=1):

Репетитор по математике о работе со слабым учеником

Несмотря на горячее желание репетитора добиться глубокого понимания всей логики операций с множествами, наибольшую эффективность для слабого ученика, как показывает практика, имеет самое обычное заучивание переходных схем. Однако добиться запоминания можно только на определенной системе упражнений. Репетиторы по математике могут комбинировать следующие виды заданий:

1) Обычное решение задач. Ребенок просто подставляет вместо знаков f (x) и g (x) соответствующие многочлены и доводит решение до ответа. Такой подход не столь эффективна в случае, если ставиться цель запомнить именно схемы. Почему? Потому, что относительное время, затрачиваемое на работу c ними крайне мало по сравнению с тем временем, которое тратится на всё задание. Альтернативой является применение одного из следующих приемов.

2) Метод частичного решения. Репетитор по математике записывает типовое неравенство и просит составить только саму систему. При этом за один урок можно обработать значительно больше переходов. Безусловно репетитор должен чувствовать ученика и не увлекаться чрезмерным количеством однотипных заданий. Почему? Потому, что отрабатывая один навык, ученик теряет другие. Для снижения этого эффекта задания должны быть двухэтапными и (или) чередующимися с аналогичными из другой темы. То есть при работе с логарифмами, нужно разбавить систему упражнений показательными или даже иррациональными неравенствами. Устойчивое запоминание чего-либо, как правило, обеспечивается многократным переключением внимание с одного объекта на другое и назад к первому. Причем важно, чтобы у ребенка был выбор: применить ли ему одно правило или применить другое. Поэтому в типовых заданиях репетитору по математике необходимо чередовать знаки неравенств или расположение степеней по отношению к единице, менять расположение левых и правых частей уравнений местами. Например квадратный корень в первом номере расположить правее знака равно, а в другом левее. Казалось бы мелочь, но она позволяет ученику развивать оценочную сторону мышления, способность распознавать объекты. Такой режим работы памяти обеспечит слабому ученику максимально долгое запоминание информации.

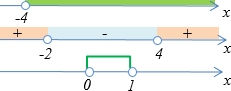
3) В чем главная цель каких-либо упражнений по математике вообще? Развитие и удержание внимание на изучаемом или запоминаемом объекте. Главная методическая проблема для репетитора состоит в крайне скудном наборе прямых задач на отработку переходов. Они включаются в состав длинных алгоритмов и не выделяются как самостоятельные триноровочные упражнения. Как я решаю эту проблему? Заметьте, что вся техника работы с переходами отрабатывается «в одну сторону», то есть дано неравенство – решаем его. Что мешает репетитору изменить этот порядок? Немного фантазии и уникальное задание готово: репетитор по математике записывает систему, а ребенок ищет чье именно решение ему показывает репетитор, например:

Здесь ученик должен составить иррациональное неравенство 2-x’ style=’vertical-align:-30%’ alt=’\sqrt>2-x’ />

Если отклониться от темы страницы, то аналогичное задание репетитор по математике может предложить в какой угодно теме, например в тригонометрии: решением какого тригонометрического уравнения является выделенная дуга?

Можно корректировать уровни заданий: легкий (на рисунке слева) и средний (на рисунке справа).

Колпаков Александр Николаевич,
репетитор по математике в Москве.
Подготовка к ЕГЭ в Строгино

Источник

Использование равносильных переходов и нестандартных приемов при решении иррациональных и логарифмических уравнений

Разделы: Математика

Цели урока:

Анализ решения уравнений при проведении ЕГЭ показывает, что с уравнениями обычно складывается странное положение. Эти задачи не считаются обычно трудными, и большинство решающих с ними, по их мнению, справляются. В то же время, многим не засчитываются эти решения из-за грубых ошибок.

Почему же так происходит?

Дело в том, что у многих, окончивших среднюю школу, имеется огромный разрыв между приобретёнными техническими, вычислительными навыками и сознательным пониманием тех теоретических и логических основ, без которых правильно решать уравнения невозможно.

Упростить уравнение с помощью безошибочно проведённых выкладок может большинство, но заметить, как и почему эти выкладки приводят к приобретению или потере решения может далеко не каждый, а очень многие об этом даже и не задумываются.

Или взять вопрос о проверке. Одни считают, что это прихоть учителей, которой нужно волей или неволей подчиняться. Другие проверяют всё подряд. Такие мнения основаны на непонимании того, что такое проверка и какое значение она должна занимать в решении.

Короче говоря, всякий должен владеть тем теоретическим минимумом, который необходим для решения уравнений.

Остановимся на этом минимуме! [1]

1. Прежде всего, что такое ОДЗ – область допустимых значений уравнения?

Областью допустимых значений (ОДЗ) уравнения называется множество значений неизвестного, при котором имеют смысл (определены) его левая и правая части.

Уравнение 1:

ОДЗ ,

ОДЗ .

При решении уравнения ОДЗ изменилась. Но это ли привело к появлению посторонних корней, мы узнаем позже.

Уравнение 2:

ОДЗ

ОДЗ

При решении уравнения ОДЗ изменилась. Но это ли привело к появлению посторонних корней, мы узнаем позже.

Прежде ответим на следующие вопросы.

2. Какое уравнение является следствием другого?.

Ответ: Если все корни первого уравнения, являются корнями второго уравнения, то второе уравнение называется следствием первого.

3. Какие уравнения являются равносильными?

Ответ: Уравнения, имеющие одно и то же множество корней, называются равносильными.

4. Какие преобразования приводят к нарушению равносильности?

Ответ: Посторонние корни могут получиться:

Все эти преобразования приводят к образованию новых корней, которые можно отбросить с помощью проверки или следить, чтобы равносильность не нарушалась.

Также равносильность может нарушиться в другую сторону, т.е. может произойти потеря корней, что потом восстановить будет невозможно. Это может быть в следующих случаях:

Ответ: Все преобразования, которые ведут к расширению области корней, или оставляют её неизменной, приводят к уравнению следствию.

6. Одинаков ли будет ответ на эти два вопроса (4 и 5)?

Ответ: как видим ответы разные.

Равносильны ли уравнения? Объясните, какое преобразование было выполнено при переходе от первого уравнения ко второму и может ли оно привести к нарушению равносильности?

Значит при переходе ко второму уравнению в случаях а), б), г) нужна оговорка (они равносильны в своей ОДЗ), а в случаях в) и д) нужно наложить условие (в случае «в»: , в случае «д»: ).

При каком условии равносильны уравнения:

Вернёмся к уравнениям:

Уравнение 1:

(I)

(II)

— посторонний корень.

Ответ: .

Вопрос: За счёт чего появился посторонний корень?

Ответ: Т.к. уравнение является уравнением следствием не только для уравнения , но и для постороннего уравнения . Таким образом при возведении в квадрат корни не теряются, но посторонние корни появиться могут.

Уравнения (I) и (II) неравносильны, но они равносильны на области .

Заменим уравнение (I) на равносильную систему:

Рассмотрим Уравнение 2:

(III)

(IV)

— посторонний корень,

Ответ: .

Вопрос: За счёт чего появился посторонний корень?

Ответ: За счёт расширения ОДЗ.

Уравнения (III) и (IV) неравносильны, но они неравносильны в ОДЗ первого уравнения, то есть заменим (III) на равносильную систему:

Рассмотрим следующие уравнения:

Уравнение 3: [3]

Уравнение 4: [3]

Уравнение 5: [3]

Все эти уравнения имеют вид .

В ОДЗ обе части неотрицательны, и возведение в квадрат даёт равносильное уравнение . Поэтому

[2]

При таком способе решения достаточно проверить неотрицательность одной из функций – можно выбрать более простую.

Применяя данный способ, решим каждое из этих уравнений.

Уравнение 3:

Ответ:

Уравнение 4:

Ответ:

Уравнение 5:

.

Перейдём к логарифмическим уравнениям:

В тетрадях своих учащихся, я встретилась со следующими решениями логарифмических уравнений. Ребята были уверены, что решили всё правильно. Получив тетрадь разочаровывались, увидев оценку ниже, чем рассчитывали. Вам предстоит найти эти ошибки:

Пример 1:

(I)

(II)

Ответ: .

Пример 2:

(I)

(II)

Т.к. , то корней нет

Ошибки состоят в следующем: в процессе решения в обоих случаях уравнение (I) заменено на уравнение (II), не являющееся его следствием. В этом случае имеется корень уравнения (I), не являющийся корнем уравнения (II). Поэтому произошла потеря корня. В примере 1 , В примере 2 .

В примере 1 корень был потерян при переходе к другому основанию логарифма. Перейдя к основанию, тем самым было исключено из ОДЗ число , которое является корнем исходного уравнения.

В примере 2, убрав показатель 4, нужно было перейти к равносильному уравнению вида

.

Подведём итог:

Таким образом, в процессе решения, каждое уравнение заменяется на какое-то новое, а у нового уравнения естественно могут быть новые корни. Проследить за изменением корней, не допустить потери и отбросить лишние корни – это и есть задача правильного решения уравнений.

Нестандартные приёмы при решении уравнений.

Кроме того, хочется сказать, что не всегда уравнения решают по алгоритму. Хотя внешний вид уравнений стандартен, но требует нестандартного подхода.

Уравнение 1: .

Решение «в лоб» даёт уравнение четвёртой степени, которое решить практически невозможно. Используем для решения метод оценки:

, , поэтому сумма.

Делаем вывод: корней нет.

Уравнение 2:

Решение: Данное уравнение можно решить стандартным способом, что приводит к «большим» числам в квадратном уравнении.

Ответ: .

Уравнение 3:

Решение: заметим, что сумма коэффициентов в каждом подкоренном выражении равна 0. Значит корень уравнения .

Возможно предположить, что ОДЗ состоит только из этого числа. Найдя ОДЗ, убеждаемся, что так оно и есть. Значит корень уравнения один .

Ответ: .

Уравнение 4:

Решение: т.к. левая часть является суммой двух неотрицательных слагаемых, то от уравнения перейдём к равносильной системе:

Ответ: .

Уравнение 5: [1]

Это уравнение можно переписать в виде

.

Итак, степени равны, основания равны. Чтобы не потерять корней, посмотрим, может ли основание быть равным 0 или 1. Так как выражение не имеет смысла, то число 0 не входит в ОДЗ, а потому не является корнем уравнения. Напротив, , очевидно, является корнем. Будем теперь искать корни, отличные от 0 и 1. Тогда, применяя указанное правило, получим , откуда находим второй корень уравнения .

Ответ: , .

Конечно, невозможно указать все методы решения «нестандартных» задач. Здесь приходится применять и графики, и самые различные свойства функций, и неравенства, и – последнее по счету, но первое по важности – логику.

Вывод: Сегодня на уроке мы постарались охватить тот минимум теоретических знаний, который необходим для решения уравнений. Знание этого минимума позволяет нам решать уравнения не допуская ошибок.

Список литературы:

Источник