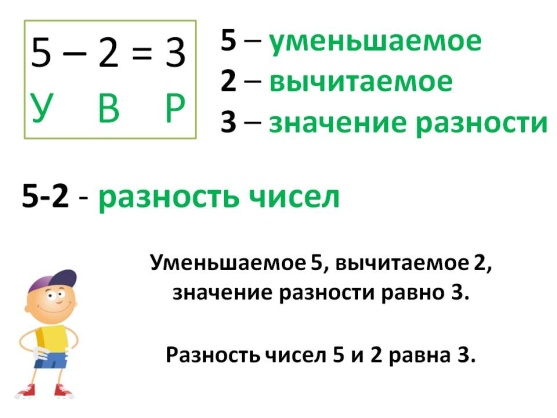
Что такое разность произведение частное
Как найти разность чисел в математике
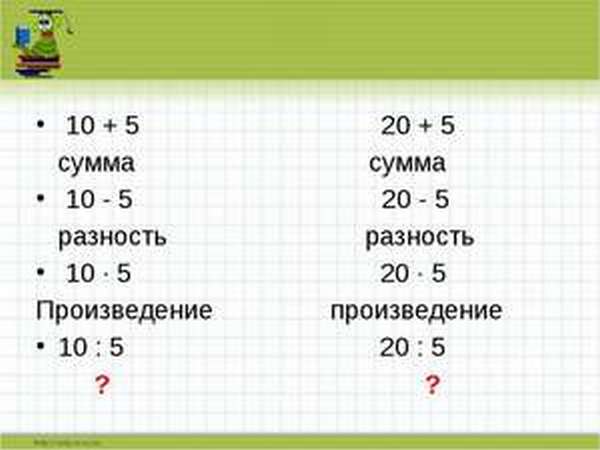
Арифметические действия с числами
Основными арифметическими действиями в математике являются:
Каждый результат этих действий также имеет своё название:
Это интересно: что такое модуль числа?
Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:
Разность в математике
Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:
И все эти определения являются верными.
Как найти разницу величин
Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:
Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:
Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?
Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:
Математические действия с разностью чисел
Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.
Простые примеры
20 — уменьшаемое значение,
Ответ: 5 — разница величин.
32 — вычитаемое значение.
Решение: 32 + 48 = 80
17 — уменьшаемая величина.
Ответ: вычитаемое значение 10.
Более сложные примеры
На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.
56 — уменьшаемое значение,
12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым),
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым),
Ответ: 40 — разница трёх значений.
Даны дроби с одинаковыми знаменателями, где
4/5 — уменьшаемая дробь,
Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.
Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5
А как выполнить такой пример, когда требуется удвоить или утроить разницу?
Вновь прибегнем к правилам:
7 — уменьшаемая величина,
5 — вычитаемая величина.
2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.
7 — уменьшаемая величина,
Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?
И опять есть применяемое для конкретного случая правило:
Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.
Математика для блондинок
В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.
И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:
Как найти разность чисел в математике
Арифметические действия с числами
Основными арифметическими действиями в математике являются:
Каждый результат этих действий также имеет своё название:
Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:
Разность в математике
Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:
И все эти определения являются верными.
Как найти разницу величин
Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:
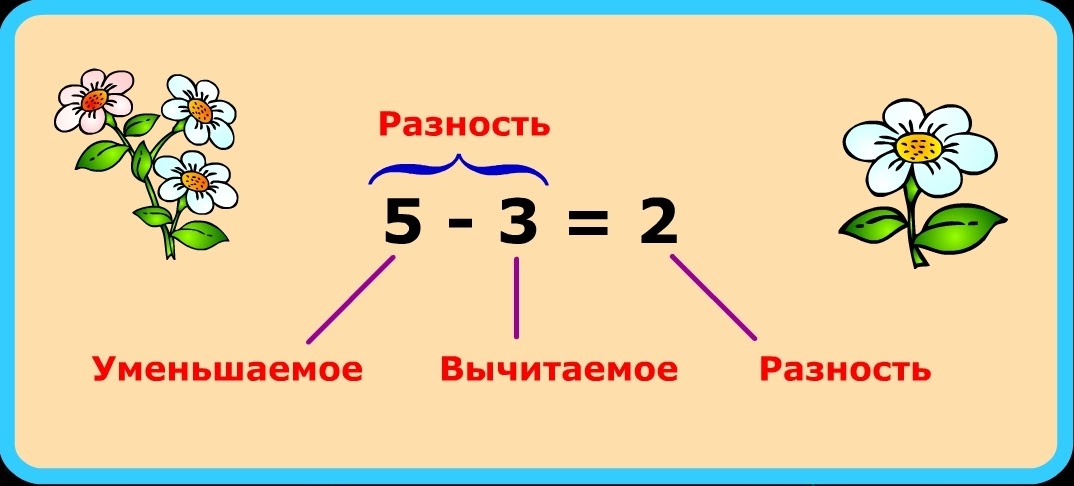
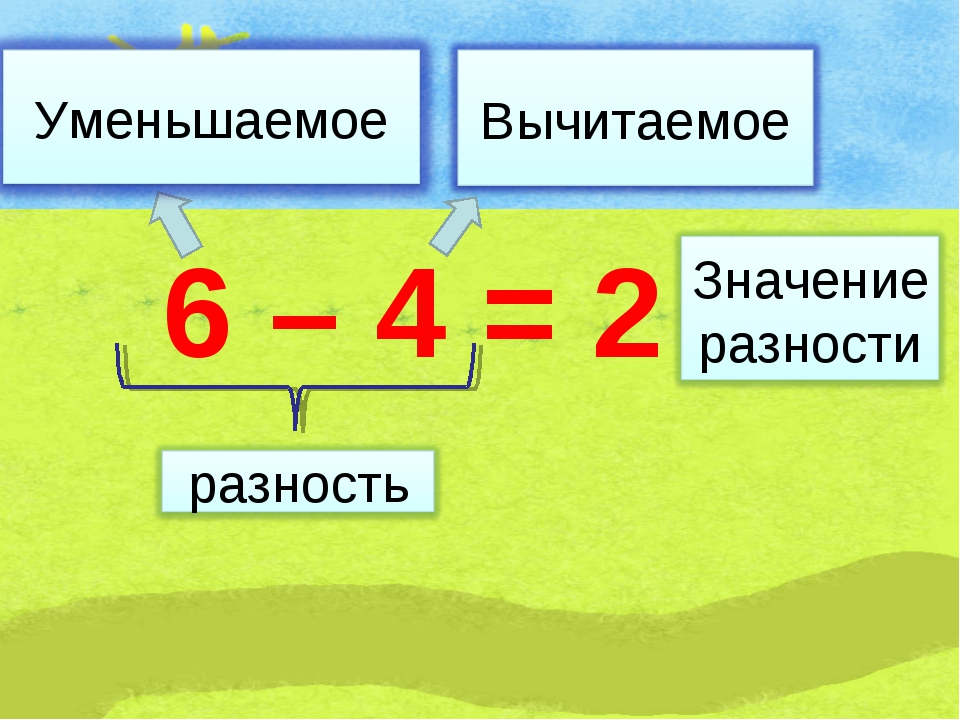
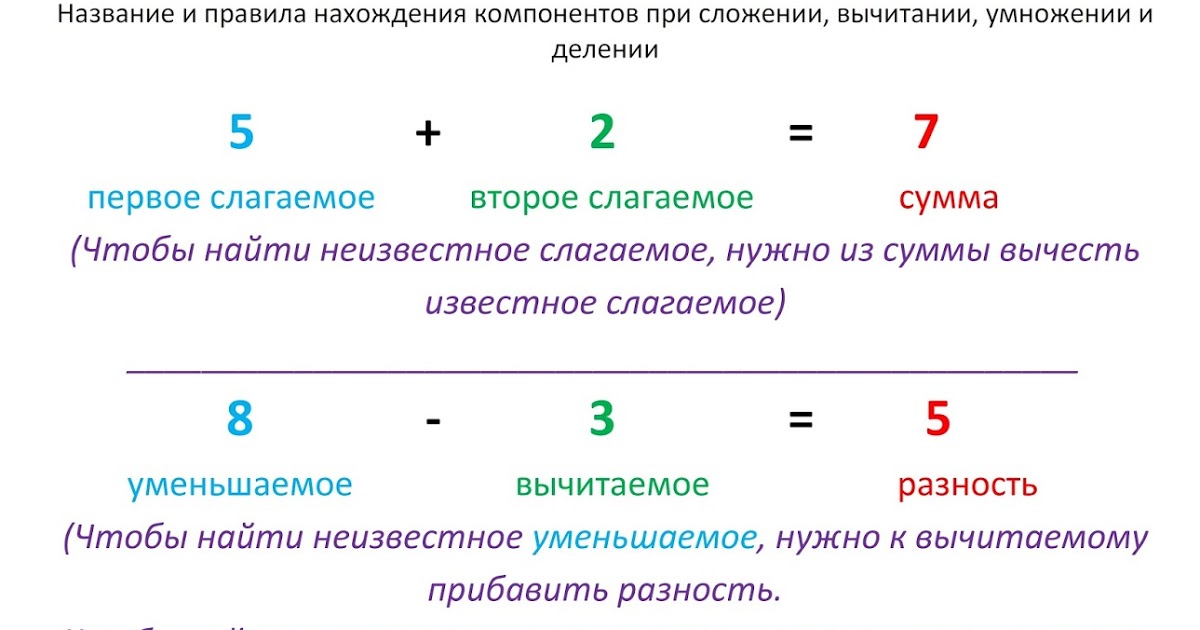
Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.
Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:
Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.
Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?
Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:
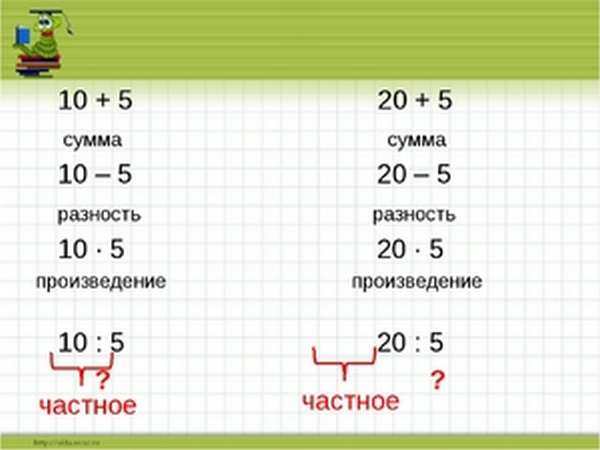
Что такое сумма, разность, произведение, частное в математике?
I. Математические понятия СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ взаимосвязаны с математическими терминами СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ, ДЕЛЕНИЕ.
Все определения даются здесь на множестве натуральных чисел.
Каждой паре чисел ставится в соответствие число, называемое их СУММОЙ.
Сумма состоит из стольких единиц, сколько их содержится в числах (слагаемых) из данной пары.
СУММА есть результат сложения чисел-слагаемых.
Вычитание — это операция, обратная сложению. Она состоит в нахождении одного из слагаемых по сумме и другому слагаемому. Данная сумма называется уменьшаемым, данное слагаемое — вычитаемым, а искомое слагаемое — РАЗНОСТЬЮ.


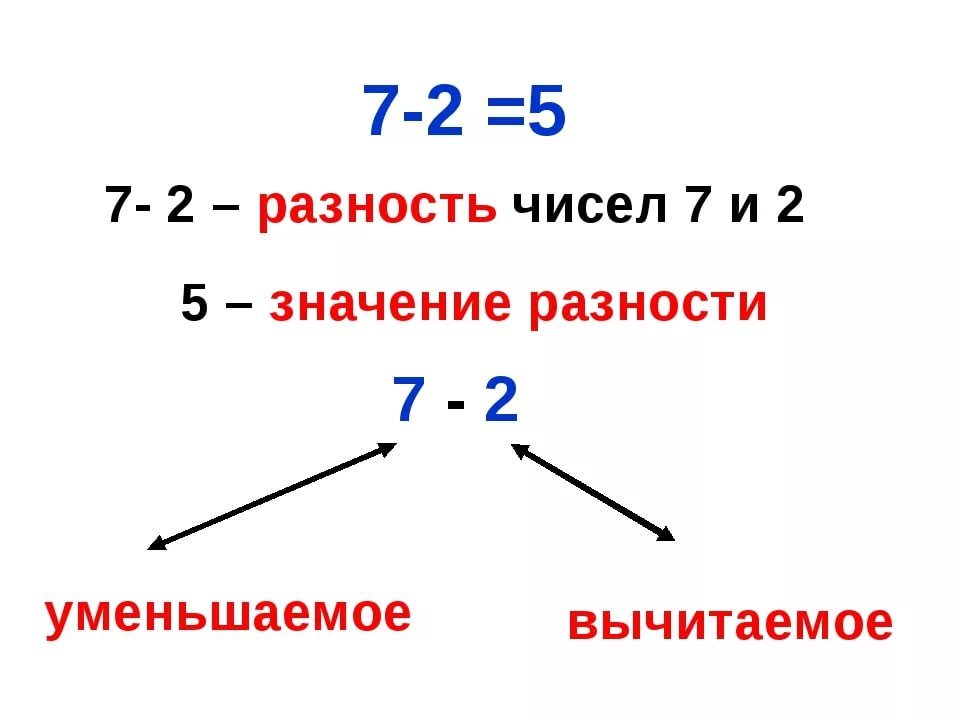





РАЗНОСТЬ — это число, являющееся результатом вычитания, остаток вычитания.
ПРОИЗВЕДЕНИЕ — это результат умножения.
Деление есть операция, обратная умножению.
Деление — это нахождение одного из сомножителей по произведению и другому сомножителю. Данное произведение называется делимым, данный сомножитель — делителем, а искомый сомножитель — это ЧАСТНОЕ, то есть число, полученное от деления одного числа на другое.
II. ДРУГИЕ ЗНАЧЕНИЯ СЛОВ СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ.
Все используемые в качестве математических понятий слова могут иметь и другие лексические значения.
СУММА в переносном значении означает совокупность, общее количество чего-либо.
Например. Профессионализм педагога заключается в сумме знаний, умений и навыков, передаваемых им своим ученикам. Отсутствие нужной суммы денег заставило отказаться от покупки.
РАЗНОСТЬ имеет значения разницы, несходства, отличия в чем-либо.
ПРОИЗВЕДЕНИЕ означает что-либо произведенное в процессе труда, создание чего-нибудь, продукт труда, творчества, искусства и т.п.
Например. Высокое художественное произведение заставляет человека думать над своей жизнью. На конкурсе юных пианистов мальчик играл произведение П.И. Чайковского. Эта шкатулка — настоящее произведение искусства.
ЧАСТНОЕ — это что-то личное, персональное, принадлежащее только одному человеку, это его собственность, его и только его достояние. И будь то самоличные мысли, будь то имущество или что-нибудь другое, но оно принадлежит только ему, частному лицу.
Например. Подруга подарила мне записную книжку с надписью «Частное». Хорошо ли противопоставлять частное общественному?
Как найти уменьшаемое и вычитаемое число?
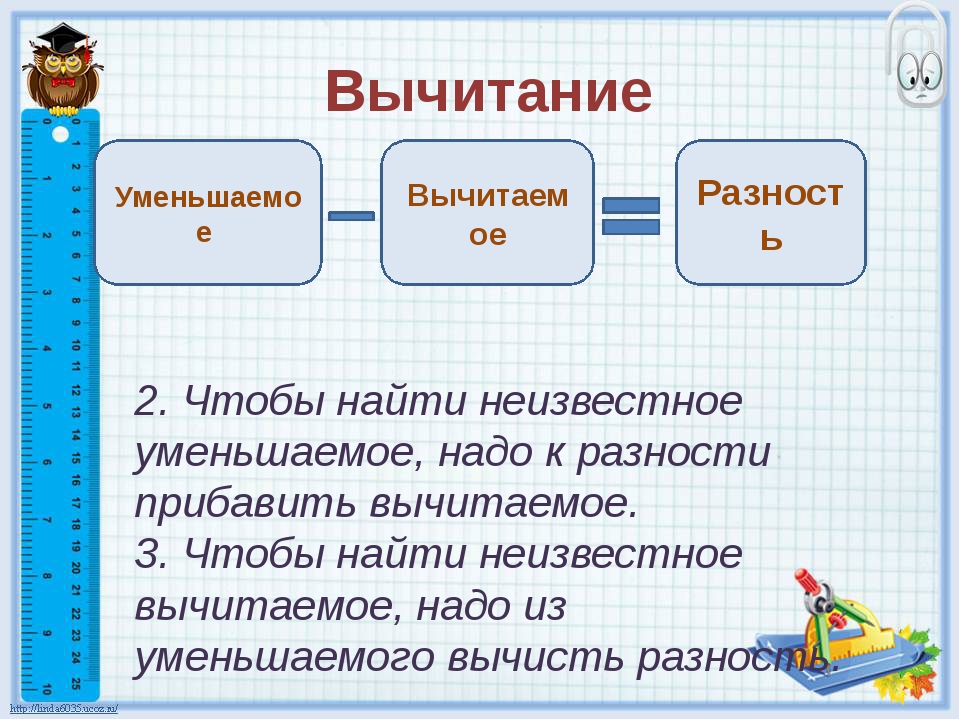
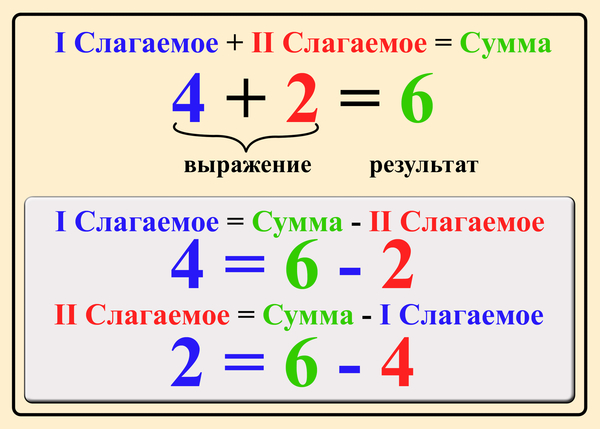
Как в математике найти разницу чисел мы уже разобрались. Это довольно просто. Но сможем ли мы найти уменьшаемое и вычитаемое число, если одно число неизвестно? Конечно можем, так как нам будут известны два других числа. Например, как мы можем найти уменьшаемое число? Если мы знаем значение разницы и вычитаемого, то сумма этих двух чисел равняется уменьшаемому:
Вычитаемое находится так же просто. Если мы знаем разницу и уменьшаемое, значит вычитаемое мы получим, отняв от уменьшаемого числа разность:

Натуральные числа
Математические действия с разностью чисел
Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.



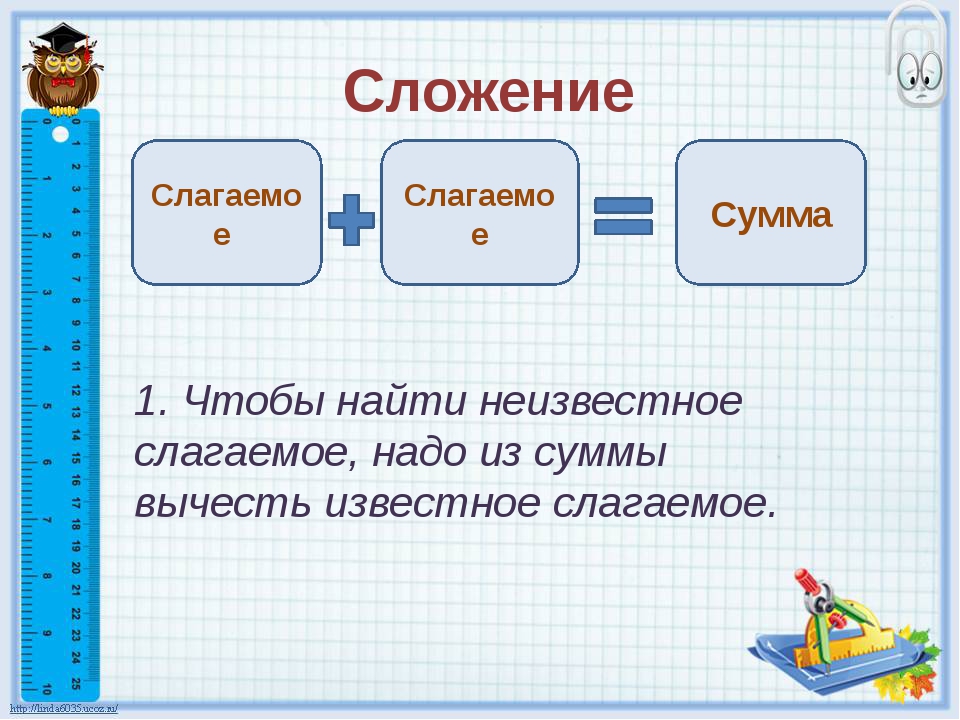

Простые примеры
Пример 1. Найти разницу двух величин.
20 — уменьшаемое значение,
Ответ: 5 — разница величин.
Пример 2. Найти уменьшаемое.
32 — вычитаемое значение.
Решение: 32 + 48 = 80
Пример 3. Найти вычитаемое значение.
17 — уменьшаемая величина.
Ответ: вычитаемое значение 10.
Более сложные примеры
На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.






Пример 4. Найти разницу трёх значений.
56 — уменьшаемое значение,
12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым),
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым),
Ответ: 40 — разница трёх значений.
Пример 5. Найти разницу рациональных дробных чисел.
Даны дроби с одинаковыми знаменателями, где
4/5 — уменьшаемая дробь,
Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.








Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5
Пример 6. Утроить разницу чисел.
А как выполнить такой пример, когда требуется удвоить или утроить разницу?
Вновь прибегнем к правилам:
7 — уменьшаемая величина,
5 — вычитаемая величина.
2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.
Пример 7. Найти разницу величин 7 и 18.
7 — уменьшаемая величина,
Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?
И опять есть применяемое для конкретного случая правило:
Если вычитаемое больше уменьшаемого, разница окажется отрицательной.
Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.
Что такое сумма, разность, произведение, частное в математике?
В каких ещё значениях, не связанных с математикой, употребляются эти слова?
Я математик по образованию, специальность: учитель математики. Проработала всю жизнь преподавателем математики в педвузе.
Необходимо оговориться. Речь в дальнейшем пойдет о сумме, разности, произведении, частном чисел.
Ответы на данные вопросы хотя и простые, но вызывают затруднения у учащихся. Чтобы можно было более подробно рассмотреть эту обобщающую тему, предлагаю вашему вниманию полезный материал по ней. Заметка называется «Математика для блондинок».
Мне понравилась методика изучения.
Задается провокационный вопрос:
Пытаются заинтересовать (ни одна предложенная версия не является верной!)))
О других значениях данных слов не задумываюсь, математика затмевает все.)))
Это такие математические понятия.
Эти все понятия проходят в начальной школе.
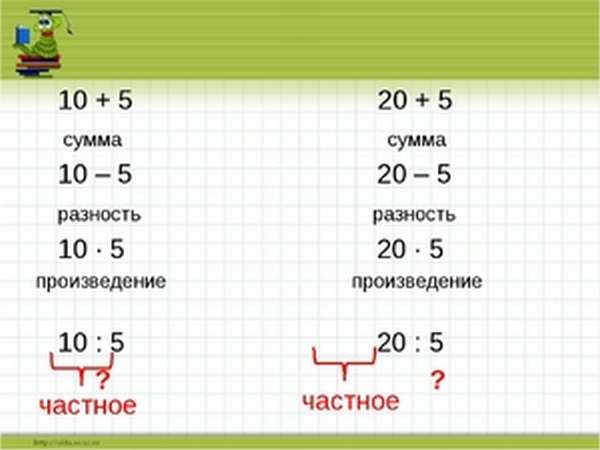
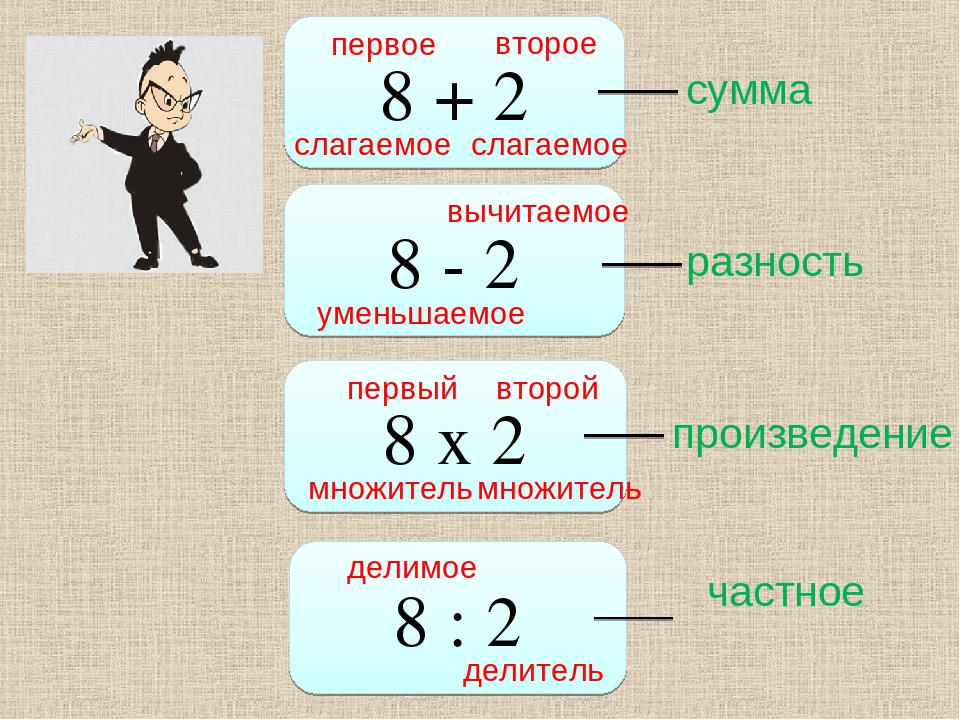
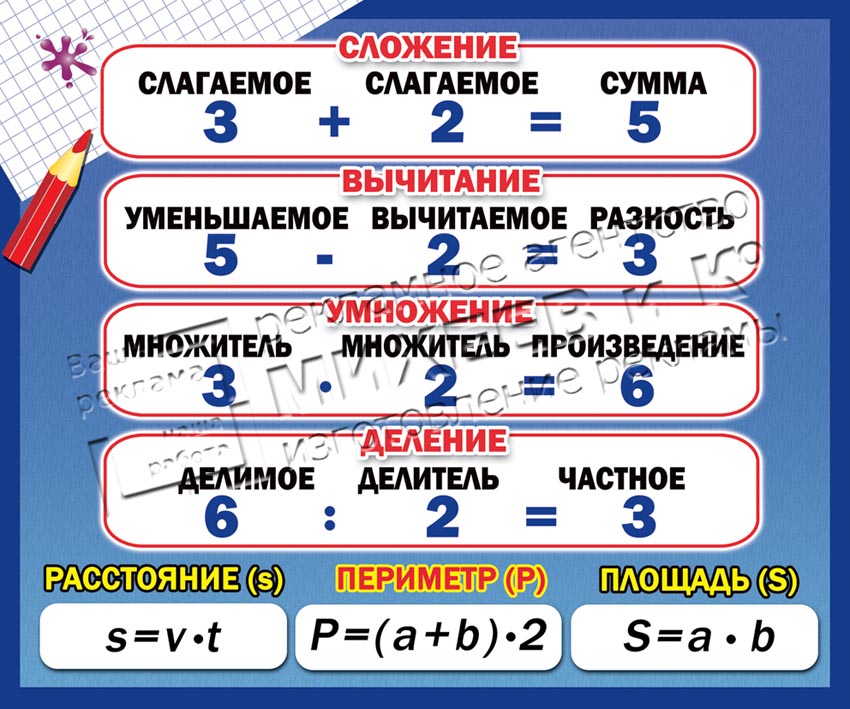
В математике есть четыре простые операции, которые можно применить к двум числам и получить такие результаты:
I. Математические понятия СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ взаимосвязаны с математическими терминами СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ, ДЕЛЕНИЕ.
Все определения даются здесь на множестве натуральных чисел.
Каждой паре чисел ставится в соответствие число, называемое их СУММОЙ.
Сумма состоит из стольких единиц, сколько их содержится в числах (слагаемых) из данной пары.
СУММА есть результат сложения чисел-слагаемых.
Каждой паре чисел можно поставить в соответствие число, которое состоит из стольких единиц, сколько их содержится в первом числе из пары, взятых столько раз, сколько единиц содержится во втором числе из пары. Это соответствующее таким образом паре чисел (они называются сомножителями) число называется ПРОИЗВЕДЕНИЕМ.
Деление есть операция, обратная умножению.
II. ДРУГИЕ ЗНАЧЕНИЯ СЛОВ СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ.
Все используемые в качестве математических понятий слова могут иметь и другие лексические значения.
СУММА в переносном значении означает совокупность, общее количество чего-либо.
Например. Профессионализм педагога заключается в сумме знаний, умений и навыков, передаваемых им своим ученикам. Отсутствие нужной суммы денег заставило отказаться от покупки.
РАЗНОСТЬ имеет значения разницы, несходства, отличия в чем-либо.
ПРОИЗВЕДЕНИЕ означает что-либо произведенное в процессе труда, создание чего-нибудь, продукт труда, творчества, искусства и т.п.
Например. Подруга подарила мне записную книжку с надписью «Частное». Хорошо ли противопоставлять частное общественному?
Частное в математике — определение, свойства и формула
Математика – царица наук. Она хоть и сложна, и многие боятся некоторых запутанных формул и вычислений, но все они состоят из простых арифметических действий сложения, вычитания, умножения и деления.
Производные операции от этих действий называются суммой, разностью, произведением и частным. Что такое частное в математике и каковы его главные свойства – будет подробно рассказано далее.
Основное свойство частного
Деление – это арифметическая операция, обратная умножению. С ее помощью можно просто узнать, сколько в первом числе содержится значений второго.
По аналогии с умножением, которое способно заменить собой многократное сложение, дробление способно заменить многократное вычитание.
Например, необходимо разделить 10 на 2. Это означает, что требуется узнать, сколько раз число 2 содержится в 10. Делая это вычитанием можно получить следующее:
10 — 2 — 2 — 2 — 2 — 2 = 0.
Проводя постепенное вычитание до нуля, можно определить, что двойка содержится в десятке ровно 5 раз и не образует остаток. Сделать это можно было однократно поделив два значения:
Частное чисел – это итог процесса деления одного значения на второе. Пример:
Одно из важнейших правил деления частного, называемое основным свойством частного, заключается в том, что если делимое и делитель умножить или разделить на одно и то же число, то итог этой операции и, соответственно частное, не изменится:
При делении числа самого на себя результатом всегда будет единица, то есть справедливо равенство:
Справедливо и другое правило: если разделить определенную величину на единицу, то итогом процесса будет сама эта величина, то есть делимое:
Увеличение или уменьшение делимого
Некоторые другие соотношения вытекают из этих. Например, если увеличить или уменьшить делимое в n раз, то в результате частное также повысится или понизится в n раз соответственно.
Изложенное правило имеет такой вид:
12 ⁄ 2 = 6 и пусть n = 3.
Проведём увеличение и уменьшение делимого:
(12∗3) /2 = 6∗3 — увеличили делимое на 3, равенство верное: 36 / 2 = 18;
(12 / 3) / 2 = 6 / 3 — уменьшили делимое на 3, равенство все равно верное: 4 / 2 = 2.
То есть, в три раза увеличив делимое, можно в три раза увеличить частное. Аналогично выполняется и уменьшение.
Увеличение или уменьшение делителя
Следующее правило звучит так: если увеличить или уменьшить делитель в n раз, то результат деления понизится или повысится в n-нное количество раз:
Для примера требуется взять частное двух значений 54 и 6:
a / b = c и пусть n = 3.
Проведём увеличение и уменьшение делителя:
54 / (6∗3) = 9 / 3 — увеличили делитель в 3 раза, равенство верное: 54 / 18 =3;
54 / (6 / 3) = 9∗3 — уменьшили делитель в 3 раза, получаем равенство: 54 / 2 = 27.
Увеличив делитель в 3 раза, во столько же раз уменьшили частное. Уменьшив делитель в три раза, делитель, напротив, увеличился в три раза.
Проверить эти «законы» можно в любом онлайн калькуляторе или вручную в уме или на бумаге.
Данные правила являются фундаментальными и составляют базу арифметики, с которой начинается математика и остальные области знаний.
Что такое разность и частное
Ответ или решение 2
Определим, что такое разность и что такое частное
Разность и частное относятся к математическим понятиям. Так же, есть такие понятия, как сумма и произведение. Все эти понятия взаимосвязаны с математическими терминами:
Определим понятие разности
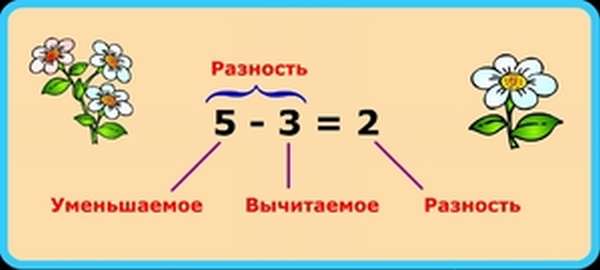
Разность – это результат действия вычитания. Разность состоит уменьшаемого, вычитаемого и разности.
Рассмотрим на примере: 9 – 3 = 6, где 9 – уменьшаемое, 3 – вычитаемое, 6 – разность. Для того, чтобы сделать проверку разности, нужно найти сумму вычитаемого и разности.
Рассмотрим примеры разностей:
Определим понятие частного
Частное – это результат действия деления. Частное состоит из делимого, делителя и частного.
Рассмотрим на примере: 15/5 = 3, где 15 – делимое, 5 – делитель, 3 – частное. Для того, чтобы сделать проверку, нужно найти произведение делителя и частного.
Рассмотрим примеры частных:
Свойства суммы, разности, произведения и частного:
Разность мы получаем в результате вычитания одного числа от другого.
Вычислим чему равна разность чисел 10 и 5.
Частное мы получаем у результате деления одного числа на другое.