Что такое разность произведение
Числовые и буквенные выражения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
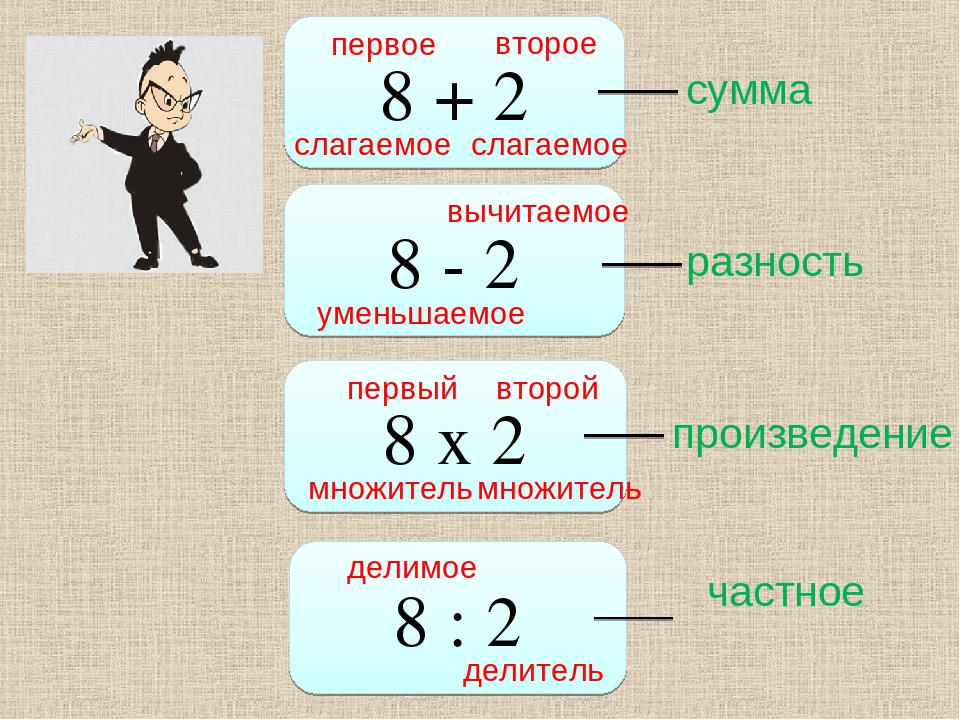
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Математика. 1 класс
Конспект урока
Математика, 1 класс
Урок № 35. Уменьшаемое. Вычитаемое. Разность. Использование этих терминов при чтении записей
Перечень вопросов, рассматриваемых в теме:
Вычитание – действие обратное сложению.
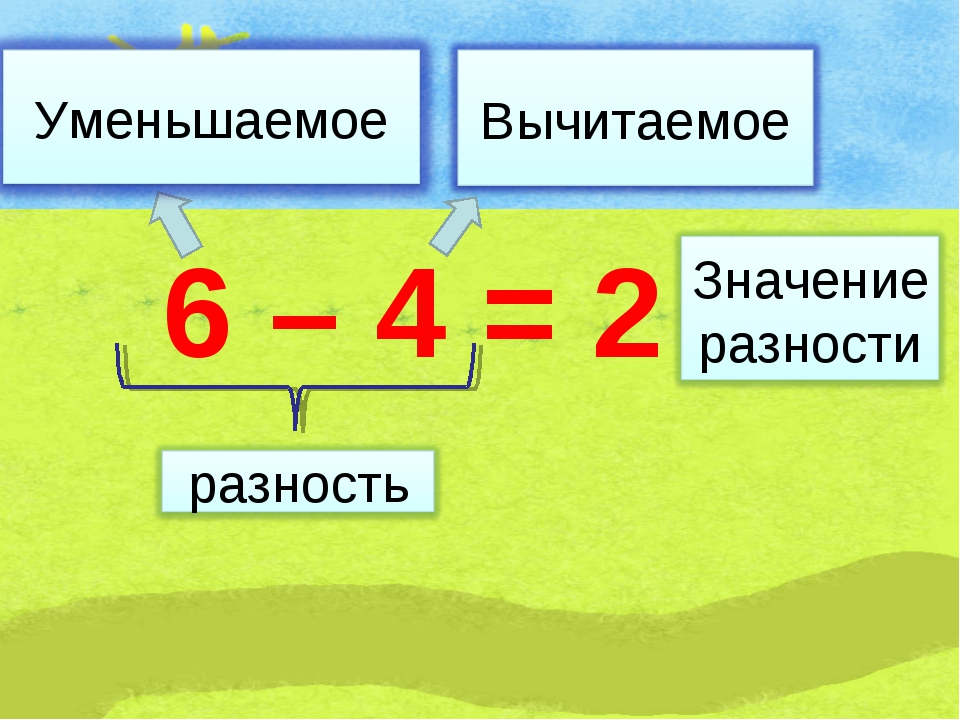
Уменьшаемое – число, из которого вычитают.
Вычитаемое – число, которое вычитают.
Разность – результат вычитания.
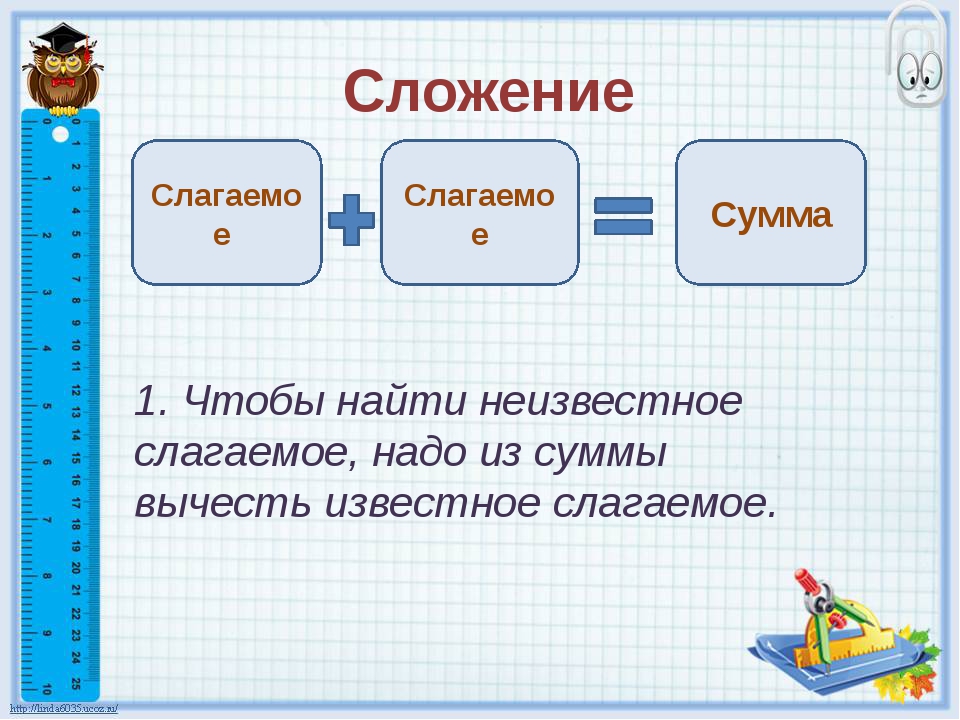
Слагаемое – число, которое складывают.
Сумма – результат сложения.
Обязательная литература и дополнительная литература:
Теоретический материал для самостоятельного изучения
Давайте решим задачу. В гараже стояли 5 машин. 2 машины уехали. Сколько машин осталось в гараже?
Для решения задачи выберем действие вычитание. Так как машины уехали, их стало меньше.
Ответ: 3 машины в гараже.
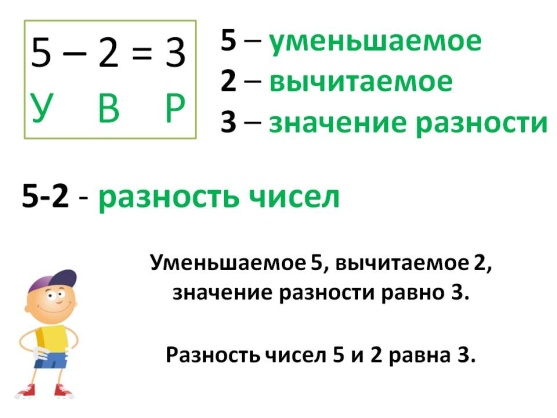
Как называются числа при вычитании?
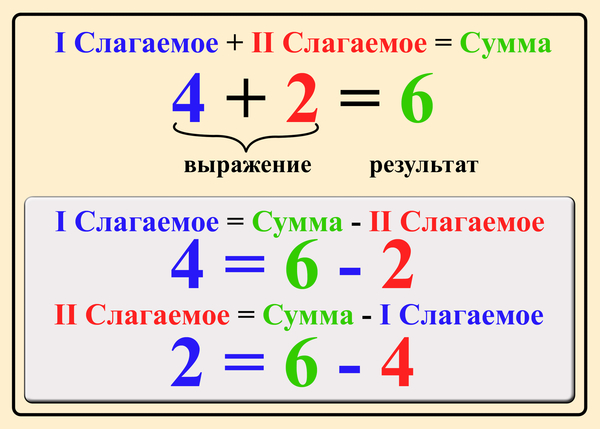
Первое число 8 – число, из которого вычитают. Это уменьшаемое.
Второе число 5 – число, которое вычитают. Это вычитаемое.
Третье число 3 – результат вычитания. Это разность.
Выражение 8 – 5 тоже называется разность.
Равенство 8 – 5 = 3 можно прочитать так. Уменьшаемое – 8, вычитаемое – 5. Разность – 3. Или, разность восьми и пяти равна трем.
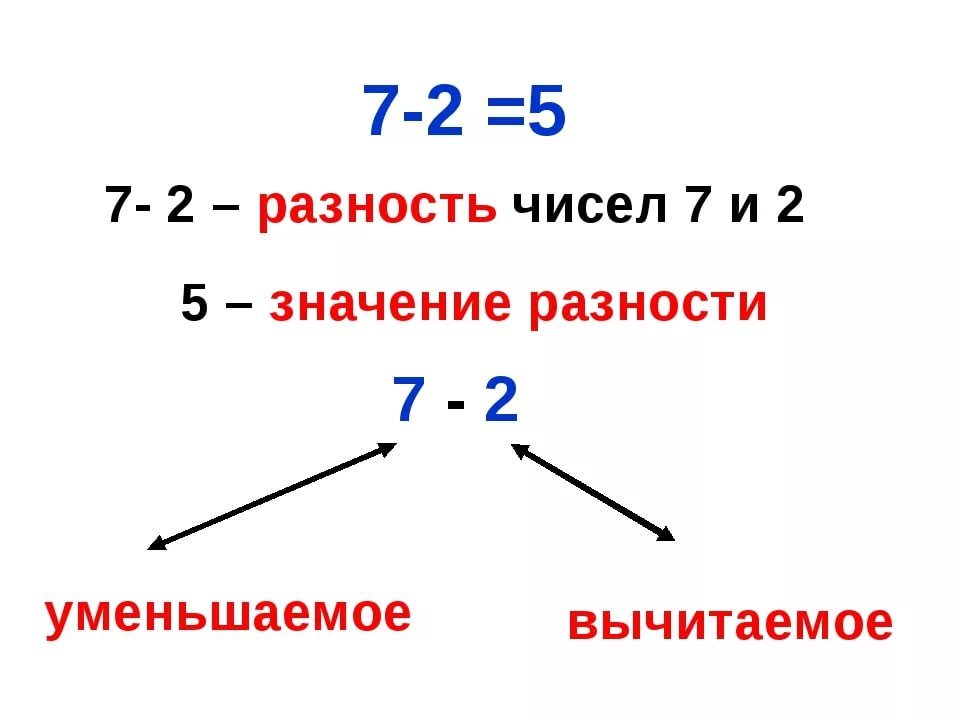
Назовем числа при вычитании.
6 – уменьшаемое, 2 – вычитаемое, 4 – разность. Выражение 6 – 2 тоже разность.
Соединим предложение с математической записью.
Уменьшаемое – 9, вычитаемое – 6. 8 – 3
Вычитаемое – 3, уменьшаемое – 8. 7 – 2
Разность чисел 7 и 2. 9 – 6
В коробке было 10 карандашей. Взяли 4 карандаша. Сколько карандашей осталось в коробке.
Для решения задачи выберем действие вычитание. Запишем разность чисел.
Ответ: 6 карандашей.
Ответим на вопросы, поставленные в начале урока.
Числа при вычитании называются уменьшаемое, вычитаемое, разность.
Уменьшаемое – число, из которого вычитают. Вычитаемое – число, которое вычитают. Разность – результат вычитания.
Выражение на вычитание можно читать по-разному. Например, 8 – 1 = 7
Уменьшаемое – 8, вычитаемое – 1, разность – 7. Или, разность чисел 8 и 1 равна 7.
Выполним несколько тренировочных заданий.
а) Вычитаемое – 3. Уменьшаемое – 5.
б) Разность чисел 7 и 2.
в) Сумма чисел 5 и 4.
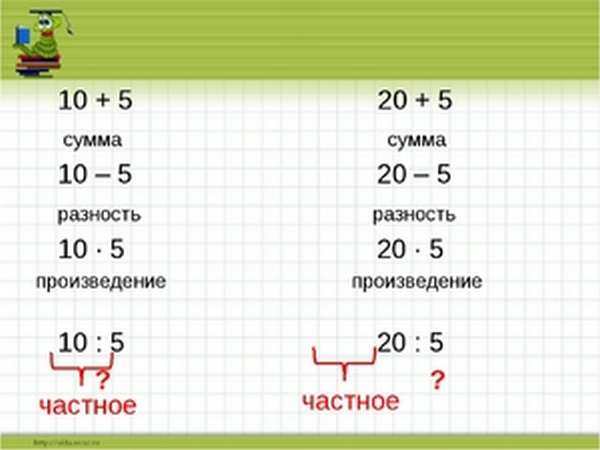
Что такое сумма, разность, произведение, частное в математике?
Что такое сумма, разность, произведение, частное в математике?
Сумма — это результат сложения, причем слово может относиться не только к цифрам.
Разность — это то, что получается после вычитания чисел.
Произведение — то что получается после умножения, слово имеет и другое значение.
Частное — это то, что получается после деления.
I. Математические понятия СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ взаимосвязаны с математическими терминами СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ, ДЕЛЕНИЕ.
Все определения даются здесь на множестве натуральных чисел.
Каждой паре чисел ставится в соответствие число, называемое их СУММОЙ.
Сумма состоит из стольких единиц, сколько их содержится в числах (слагаемых) из данной пары.
СУММА есть результат сложения чисел-слагаемых.
Вычитание — это операция, обратная сложению. Она состоит в нахождении одного из слагаемых по сумме и другому слагаемому. Данная сумма называется уменьшаемым, данное слагаемое — вычитаемым, а искомое слагаемое — РАЗНОСТЬЮ.
РАЗНОСТЬ — это число, являющееся результатом вычитания, остаток вычитания.
Каждой паре чисел можно поставить в соответствие число, которое состоит из стольких единиц, сколько их содержится в первом числе из пары, взятых столько раз, сколько единиц содержится во втором числе из пары. Это соответствующее таким образом паре чисел (они называются сомножителями) число называется ПРОИЗВЕДЕНИЕМ.
ПРОИЗВЕДЕНИЕ — это результат умножения.
Деление есть операция, обратная умножению.
Деление — это нахождение одного из сомножителей по произведению и другому сомножителю. Данное произведение называется делимым, данный сомножитель — делителем, а искомый сомножитель — это ЧАСТНОЕ, то есть число, полученное от деления одного числа на другое.
II. ДРУГИЕ ЗНАЧЕНИЯ СЛОВ СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ.
Все используемые в качестве математических понятий слова могут иметь и другие лексические значения.
СУММА в переносном значении означает совокупность, общее количество чего-либо.
Например. Профессионализм педагога заключается в сумме знаний, умений и навыков, передаваемых им своим ученикам. Отсутствие нужной суммы денег заставило отказаться от покупки.
РАЗНОСТЬ имеет значения разницы, несходства, отличия в чем-либо.
ПРОИЗВЕДЕНИЕ означает что-либо произведенное в процессе труда, создание чего-нибудь, продукт труда, творчества, искусства и т.п.
Например. Высокое художественное произведение заставляет человека думать над своей жизнью. На конкурсе юных пианистов мальчик играл произведение П.И. Чайковского. Эта шкатулка — настоящее произведение искусства.
ЧАСТНОЕ — это что-то личное, персональное, принадлежащее только одному человеку, это его собственность, его и только его достояние. И будь то самоличные мысли, будь то имущество или что-нибудь другое, но оно принадлежит только ему, частному лицу.
Например. Подруга подарила мне записную книжку с надписью «Частное». Хорошо ли противопоставлять частное общественному?
По сути, все четыре слова в вопросе, а именно сумма, разность, произведение и частное, отражаю четыре основные математические действия, которые являются азами. Именно с обучения данным действиям начинается увлекательный путь в мир математики. Таким образом,
Сумма, разность, произведение, частное — это результат математических дейтсвий, с которых мы все начинали свое знакомства с математикой. В жизни эти слова мы тоже используем, но значение вкладываем в них больше математическое, хоть складывать можем и не числа. Произведение еще может быть и художественным. Это совсем другое значение слова, которое мы применяем в жизни.
Все эти четыре термина употребляются преимущественно в математике.
Сумма — это когда происходит складывание двух чисел;
Разность- это вычитание одного числа из другого;
Частное — это деление одного числа на другое;
Произведение — это умножение одного числа на другое.
Частное — результат деления чисел, произведение — результат умножения чисел, сумма — результат сложения чисел, разность — результат вычетания. Это элементарные математические действия, которые можно проводить с числами.
Это такие математические понятия.
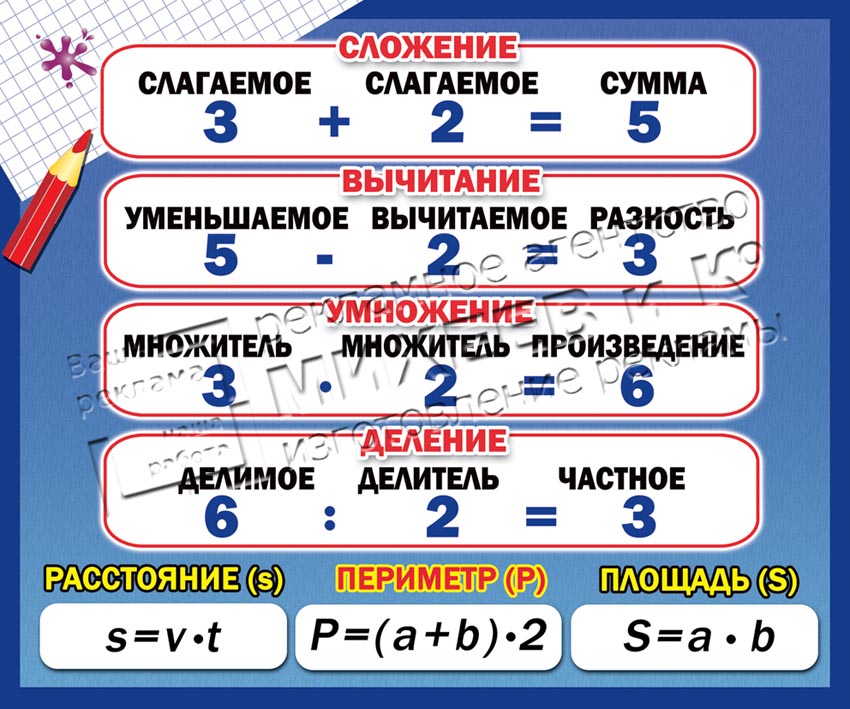
Сумма — это результат сложения. Числа, которые складывают, называют первое слагаемое и второе слагаемое. Обозначается таким знаком: +.
Произведение — это результат умножения. Числа, которые умножают, называются первым множителем и вторым множителем. Обозначается таким знаком: *.
Частное — это результат деления. Числа, которые делят, называются делимое (то, которое больше), делитель (то, которое меньше). Обозначается таим знаком: :.
Эти все понятия проходят в начальной школе.
В математике есть четыре простые операции, которые можно применить к двум числам и получить такие результаты:
сумма — это результат сложения чисел,
разность — это результат вычетания от одного числа другого,
произведение — это результат умножения чисел,
частное — это уже результат деления чисел.
Суммой в математике назовем число, которое получим в результате прибавления одного числа к другом. Разность это число противоположное сложению, это когда отнимают от большего числа меньшее. Произведением назовем число, которое получится в результате умножения одного числа на другое. Разность это противомоложное произведению число. Получаем разность так: делим одно число на другое.
Я математик по образованию, специальность: учитель математики. Проработала всю жизнь преподавателем математики в педвузе.
Необходимо оговориться. Речь в дальнейшем пойдет о сумме, разности, произведении, частном чисел.
Ответы на данные вопросы хотя и простые, но вызывают затруднения у учащихся. Чтобы можно было более подробно рассмотреть эту обобщающую тему, предлагаю вашему вниманию полезный материал по ней. Заметка называется «Математика для блондинок».
Мне понравилась методика изучения.
Задается провокационный вопрос:
Разность — это поделить или умножить?
Пытаются заинтересовать (ни одна предложенная версия не является верной!)))
Разность — это отнять. Результат вычитания называется разность.
Сумма — это сложить. Результат сложения называется сумма.
Произведение — это умножить. Результат умножения называется произведение.
Частное — это деление. Результат деления называется частное.
Таким простым языком объясняются верные понятия суммы, разности, произедения и частного в математике. Немного упрощенно записаны лишь словосочетания: разность — это отнять, сумма — прибавить, произведение — умножить, частное — разделить. Если быть точными, так не утверждают.
Итак, результат сложения чисел (слагаемых) — это их сумма, результат вычитания чисел (уменьшаемого и вычитаемого) — это разность, результат умножения чисел (сомножителей) — это произведение, а результат деления чисел (делимого на делитель), причем делитель не должен быть равен нулю, иначе деление нельзя выполнить, есть частное этих чисел.
О других значениях данных слов не задумываюсь, математика затмевает все.)))
Слова Сумма, Разность, Произведение и Частное очень знакомо ученикам школ и других учебных заведений веди с этими определениям им приходиться на каждом уроке математики.
1) Сумма
Суммой является результат, полученный после сложения (+) двух или более чисел.
Суммой так же является итоговая стоимость товара (сумма к оплате), общая совокупность знаний, впечатлений и много чего.
2) Разность
В математике означает результат вычитания числе (-).
Слово разность так же может употребляться в качестве слова разницы чего-либо. Например, разность мнений, разность взглядов, разность показателей и т.д.
3) Произведение
Произведением является результат, полученный после умножения чисел (*).
Кроме математики это слово еще употребляется в качестве обозначения результата творческого процесса (произведение искусства), в качестве глагола от «производить».
4) Честное
Этим словом обозначают результат деления двух чисел (:).
Слово «частное» мы так же можем услышать при обозначении принадлежности чего либо одному собственнику (частное лицо, частная собственность, частное дело).
Как найти разность чисел в математике
Арифметические действия с числами
Основными арифметическими действиями в математике являются:
Каждый результат этих действий также имеет своё название:
Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:
Разность в математике
Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:
И все эти определения являются верными.
Как найти разницу величин
Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:
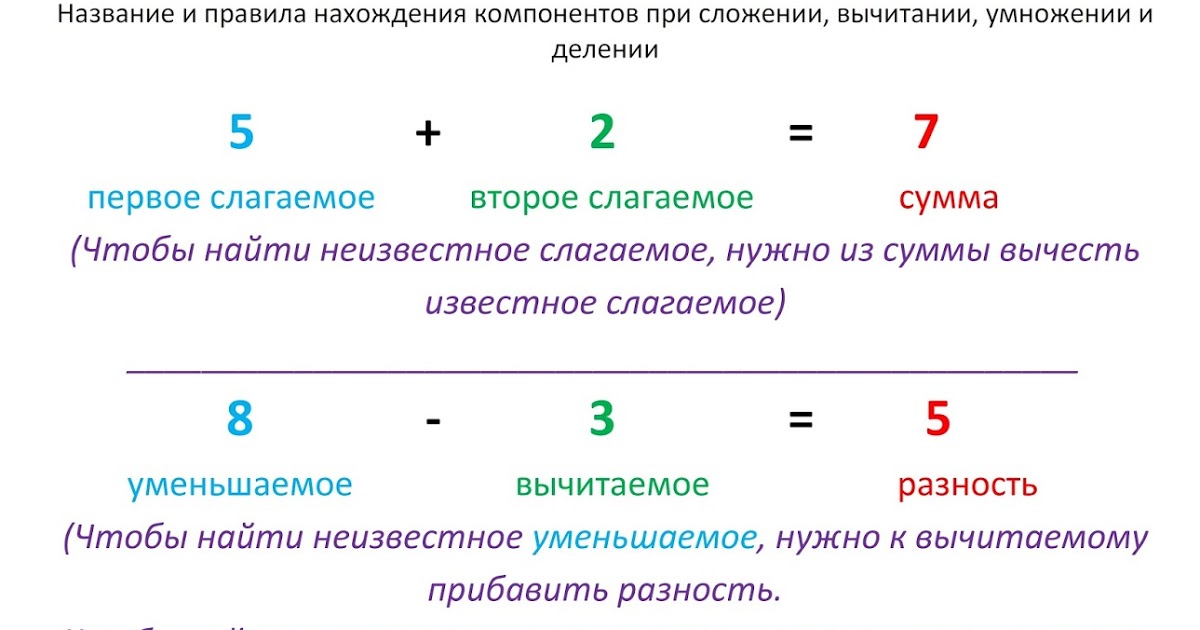
Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.
Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:
Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.
Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?
Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:
Что такое сумма, разность, произведение, частное в математике?
I. Математические понятия СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ взаимосвязаны с математическими терминами СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ, ДЕЛЕНИЕ.
Все определения даются здесь на множестве натуральных чисел.
Каждой паре чисел ставится в соответствие число, называемое их СУММОЙ.
Сумма состоит из стольких единиц, сколько их содержится в числах (слагаемых) из данной пары.
СУММА есть результат сложения чисел-слагаемых.
Вычитание — это операция, обратная сложению. Она состоит в нахождении одного из слагаемых по сумме и другому слагаемому. Данная сумма называется уменьшаемым, данное слагаемое — вычитаемым, а искомое слагаемое — РАЗНОСТЬЮ.







РАЗНОСТЬ — это число, являющееся результатом вычитания, остаток вычитания.
ПРОИЗВЕДЕНИЕ — это результат умножения.
Деление есть операция, обратная умножению.
Деление — это нахождение одного из сомножителей по произведению и другому сомножителю. Данное произведение называется делимым, данный сомножитель — делителем, а искомый сомножитель — это ЧАСТНОЕ, то есть число, полученное от деления одного числа на другое.
II. ДРУГИЕ ЗНАЧЕНИЯ СЛОВ СУММА, РАЗНОСТЬ, ПРОИЗВЕДЕНИЕ, ЧАСТНОЕ.
Все используемые в качестве математических понятий слова могут иметь и другие лексические значения.
СУММА в переносном значении означает совокупность, общее количество чего-либо.
Например. Профессионализм педагога заключается в сумме знаний, умений и навыков, передаваемых им своим ученикам. Отсутствие нужной суммы денег заставило отказаться от покупки.
РАЗНОСТЬ имеет значения разницы, несходства, отличия в чем-либо.
ПРОИЗВЕДЕНИЕ означает что-либо произведенное в процессе труда, создание чего-нибудь, продукт труда, творчества, искусства и т.п.
Например. Высокое художественное произведение заставляет человека думать над своей жизнью. На конкурсе юных пианистов мальчик играл произведение П.И. Чайковского. Эта шкатулка — настоящее произведение искусства.
ЧАСТНОЕ — это что-то личное, персональное, принадлежащее только одному человеку, это его собственность, его и только его достояние. И будь то самоличные мысли, будь то имущество или что-нибудь другое, но оно принадлежит только ему, частному лицу.
Например. Подруга подарила мне записную книжку с надписью «Частное». Хорошо ли противопоставлять частное общественному?
Как найти уменьшаемое и вычитаемое число?
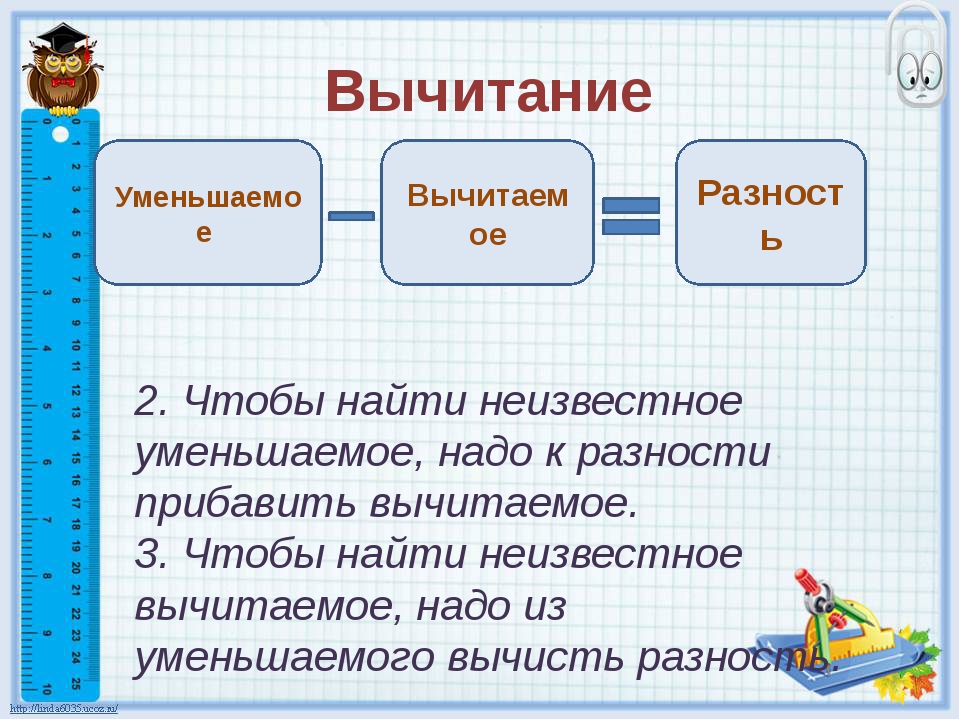
Как в математике найти разницу чисел мы уже разобрались. Это довольно просто. Но сможем ли мы найти уменьшаемое и вычитаемое число, если одно число неизвестно? Конечно можем, так как нам будут известны два других числа. Например, как мы можем найти уменьшаемое число? Если мы знаем значение разницы и вычитаемого, то сумма этих двух чисел равняется уменьшаемому:
Вычитаемое находится так же просто. Если мы знаем разницу и уменьшаемое, значит вычитаемое мы получим, отняв от уменьшаемого числа разность:

Натуральные числа
Математические действия с разностью чисел
Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.

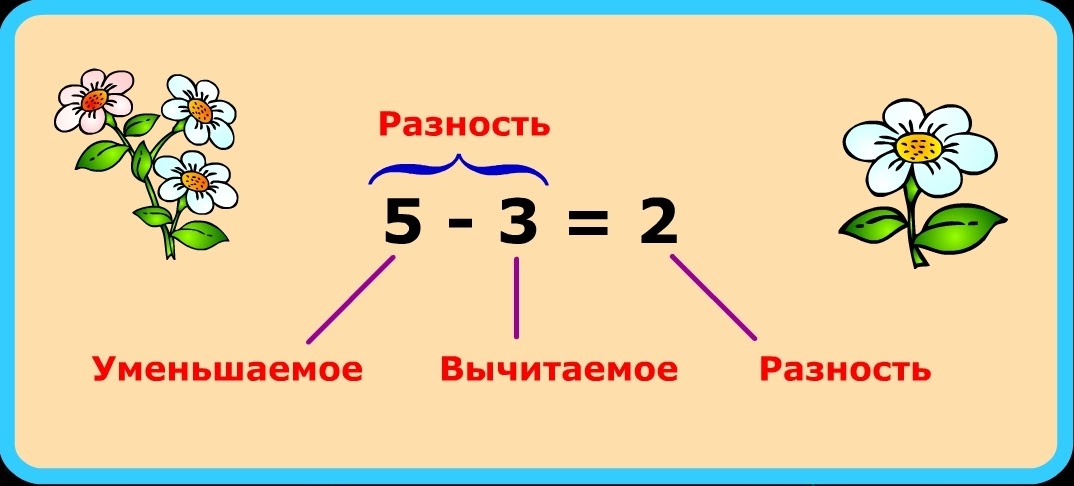



Простые примеры
Пример 1. Найти разницу двух величин.
20 — уменьшаемое значение,
Ответ: 5 — разница величин.
Пример 2. Найти уменьшаемое.
32 — вычитаемое значение.
Решение: 32 + 48 = 80
Пример 3. Найти вычитаемое значение.
17 — уменьшаемая величина.
Ответ: вычитаемое значение 10.
Более сложные примеры
На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.






Пример 4. Найти разницу трёх значений.
56 — уменьшаемое значение,
12 и 4 — вычитаемые значения.
Решение можно выполнить двумя способами.
1 способ (последовательное отнимание вычитаемых значений):
1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым),
2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):
1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым),
Ответ: 40 — разница трёх значений.
Пример 5. Найти разницу рациональных дробных чисел.
Даны дроби с одинаковыми знаменателями, где
4/5 — уменьшаемая дробь,
Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.








Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5
Пример 6. Утроить разницу чисел.
А как выполнить такой пример, когда требуется удвоить или утроить разницу?
Вновь прибегнем к правилам:
7 — уменьшаемая величина,
5 — вычитаемая величина.
2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.
Пример 7. Найти разницу величин 7 и 18.
7 — уменьшаемая величина,
Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?
И опять есть применяемое для конкретного случая правило:
Если вычитаемое больше уменьшаемого, разница окажется отрицательной.
Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.