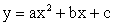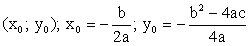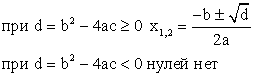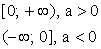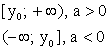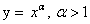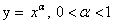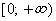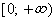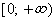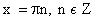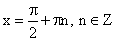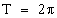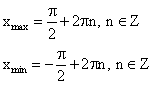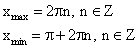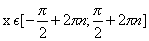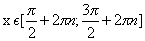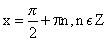Что такое свойства в алгебре
Свойства
Если после изучения данного теоретического материала у Вас возникнут проблемы в решении задач или появятся вопросы образовательного характера, то вы всегда можете задать их на нашем форуме.
Остались вопросы?
Здесь вы найдете ответы.
Поможем выполнить
любую работу
Поможем написать реферат или решить контрольную
Наши эксперты помогают подготовиться к сдаче курсовой, защите дипломной, решить задачу или написать реферат
Поможем в короткие сроки
Наши эксперты заботятся о том, чтобы помочь вам как можно скорее (от 3 часов) и делают все, чтобы вы сдали работу вовремя
Мы проверяем каждую работу на плагиат и помогаем писать «с нуля»
Наш отдел контроля качества проверит каждую запятую в вашей работе и при необходимости бесплатно внесет корректировки в течение гарантийного срока
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
Что такое свойства в алгебре
Функция
Область определения
Вершина параболы
Нули функции
Экстремумы
если a 0, то максимум в вершине
Область значений
Четность
ни четная, ни нечетная
Функция
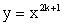
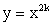
Область определения
Область значений
Четность
Нули функции
Экстремумы
х = 0 — точка минимума
Монотонность
возрастает при х ϵ R
при х ≤ 0 убывает
при х > 0 возрастает
Функция
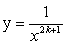
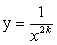
Область определения
Область значений
Четность
Нули функции
Экстремумы
Монотонность
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
возрастает при х ϵ D(f)
возрастает при х ϵ D(f)
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
Функция
Область определения
Область значений
Нули функции
Экстремумы
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
Функция
Область определения
Область значений
Нули функции
Четность
Периодичность
Экстремумы
Монотонность
Функция
Область определения
R кроме 
R кроме 
Основные свойства функций. Справочник репетитора по математике
Д анная страница справочника представляет собой виртуальную шпаргалку по математике для учеников и методическое справочное пособие для репетиторов. Тема «свойства функций», адаптированное для разных уровней учащихся 8-9класов. В нем перечислены определения основных понятий и свойств, виды функций, термины и обозначения, принятые в математике. Репетитору по математике показаны образцы рисунков, которые должны остаться в теради ученика. Информация изложена как на строгом и формальном математическом языке (для среднего и сильного ученика), так на простом (бытовом) уровне, доступном для понимания широкому кругу посетителей сайта. Каждый такой перевод с математического языка на русский отмечен одним из следующих указателей: «пояснение репетитора по математике», «редакция репетитора по математике» или «уточнение репетитора по математике». В этих — переводах вы встретите несколько моих собственных уникальных дополнений и комментариев к классическим фомулировкам, которые я использую на занятиях со слабым учеником.
Определение функции: функцией или функциональной зависимостью называется такое соответствие f (x) при котором числу x из множества X сопоставляется некоторое единственное число из множества Y.
Редакция репетитора по математике: функцией называется закон или правило, по которому можно найти число y (значение какой-нибудь величины), если известно число x (значение какой-нибудь другой величины).
При этом букву x называют независимой переменной (или аргументом), а букву y — зависимой переменной. Число, которое подставляется вместо x, называется значением переменной (или значением аргумента), а число y, которому оно соответствует, называется значением функции.
График функции — множество точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Свойства функции:
1) Что такое область определения функции? Область определения функции (О.О.Ф) — это множество всех значений переменной x, которые имеют соответствующие им значения функции.
Редакция репетитора по математике: область определения — множество значений переменной x, у которых можно найти y.
Обозначения области определения Для обозначения области определения используются следующие знаки: 
Как найти область определения по графику? Область определения — это промежутки на оси Ох, над которыми (или под которыми) имеются части графика.
2) Что такое область значений функции? Областью значений функции (О.З.Ф) называется множество всех ее значений.
Редакция репетитора по математике:областью значений функции можно назвать часть оси ОY, состоящую из игреков, у которых есть соответствующие им иксы.
Как найти область значений по графику?: область значений функции — это промежутки на оси OY, слева или справа от которых (в горизонтальной полоске) находятся части графика.
3) Возрастание и убывание функции.
Какая функция называется возрастающей?Функция 
называется возрастающей, если для любой пары значений аргументов 
и 
из неравенства 
следует неравенство 
.
Редакция репетитора по математике: Функцию можно назвать возрастающей на промежутке, если, большему из любых двух взятых из него чисел всегда соответствует большее значение функции. Для графика это будет означать то, что при движении по нему карандашом слева направо карандаш будет подниматься вверх.
Какая функция называется убывающей? Функция называется убывающей, если для любой пары значений аргументов и из неравенства следует неравенство 
f (x_2)’ style=’vertical-align:-30%’ alt=’f (x_1)>f (x_2)’ />.
Редакция репетитора по математике: Функцию можно назвать убывающей на промежутке, если большему из любых двух взятых из него чисел всегда соответствует меньшее значение функции. Для графика это будет означать, что при движении по нему карандашом слева направо карандаш будет опускаться вниз.
Можно предложить еще один вариант этого определения: функция называется возрастающей на промежутке, если знак которым связаны любые два числа ее области определения, противоположен тому, которым связаны соответствующие им значения функции.
4) Промежутки знакопостоянства — промежутки, на которых функция имеет постоянный знак (положительный или отрицательный).
Пояснения репетитора по математике: Промежуток положительного знака — это множество значений переменной x, у которых соответствующие значения функции больше нуля (y>0 ).
Как найти все такие промежутки по графику? Определите промежутки оси ОХ, у которых соответствующие кусочки графика выше оси Ох.
Как их найти без графика? составьте и решите неравенство f (x)>0
Оформление: 
o ‘ style=’vertical-align:-5%’ alt=’y>o ‘ />, если 
Промежуток отрицательного знака — это множество тех значений переменной х, у которых соответствующие значения функции меньше нуля (y
Свойство
Сво́йство (в философии, математике и логике) — атрибут предмета (объекта). Например, о красном предмете говорится, что он обладает свойством «красноты». Свойство можно рассматривать как форму предмета самого по себе, притом, что он может обладать и другими свойствами. Свойства, следовательно, подпадают под действие парадокса Рассела и парадокса Греллинга-Нельсона.
По другому определению, свойство — сторона проявления качества. При этом не всякое свойство предмета (объекта) должно рассматриваться при определении качества: свойство у предмета может иметься, но при сравнении предмета с другими оно может не быть отличительным или существенным.
Свойства объекта зависят от вида взаимодействия объекта и субъекта, например: если на яблоко смотреть — оно имеет цвет и форму; если его откусить — имеет твёрдость и вкус; если его взвешивать — имеет вес; если оценивать его габариты — имеет размеры, если трогать — имеет шероховатость. Объект является своими свойствами не только субъекту, но и другим объектам, то есть свойства могут проявляться и в ходе взаимодействия объектов друг с другом.
Совокупность некоторых частных свойств предмета может проявляться в некотором обобщённом свойстве предмета (поглощаться обобщённым свойством). Например, «краснота» яблока — обобщённое свойство яблока, а процентные доли содержания отдельных химических веществ в кожице яблока (характеризующие эту «красноту» яблока) — частные свойства яблока; «динамика» автомобиля — обобщённое свойство автомобиля, а мощность двигателя, снаряжённая масса, отношение главной передачи и др. (характеризующие эту «динамику» автомобиля) — частные свойства автомобиля.
Свойство отличается от логического понятия класса тем, что не связано с понятием экстенсиональности, а от философского понятия класса — тем, что свойство рассматривается в качестве отличного (отделённого) от предмета, который обладает им.
Содержание
В логике
В логике, основанной на булевой алгебре, понятие «свойство» совпадает с понятием «высказывание».
В математике
В математике если дан любой элемент множества X, то определённое свойство p либо истинно, либо ложно, то есть понятие «свойство» совпадает с понятием «подмножество». На формальном языке: свойство p: X → <истинно, ложно>(то есть отображение, функция из Х в множество из двух элементов). Всякое свойство естественным образом задаёт подмножество
Применение
Свойства используются в науке для образования понятий. Свойства объектов и ситуаций широко применяются в теории решения задач, в процессах автоматизации производства, управления и поиска информации, при построении экспертных систем.
Функция в алгебре: её свойства, определение и понятие
Одним из основных понятий в математике, если не самым основным, является понятие функции. Для понимания этого термина, его значения, смысла и необходимости, обратимся к следующему примеру:
Вообразим себе обыкновенный автомобиль. Предположим, что он постоянно двигается со скоростью 80 км/ч и не меняет её на протяжении всего пути. А теперь попробуем выяснить: сколько километров проедет автомобиль, если в пути он будет находиться 5 часов? Итак, нам известна скорость и время. Попробуем составить зависимость:
| Сколько времени находится в пути автомобиль? | Сколько километров автомобиль проехал? |
| 1 ч | 80 км |
| 2 ч | 160 км |
| 3 ч | 240 км |
| 4 часа | 320 км |
| 5 часов | 400 км |
Нам были известны всего две величины: скорость автомобиля и время, которое он находился в пути. Взглянув на таблицу, можно понять, что между временем, которое находился автомобиль в пути, и пройденным им расстоянием есть чёткая зависимость — каждый час автомобиль проезжает на 80 километров больше. Что ж, давайте немного приблизимся к алгебре и введём две переменные: y и x.
Y это наше расстояние, а x — время пути. Составим уравнение: y = 80 * x. Теперь вместо x подставим время:
Теперь введём следующую запись: y(x). Эта запись означает зависимость первой переменной от второй, а наше окончательное уравнение для движения автомобиля будет выглядеть следующим образом: y(x)=80x. Y в алгебре принято называть функцией, а x аргументом.
Это интересно: какой вектор называется разностью двух векторов?
Смысл
Пользуясь приведённым примером, мы чётко и ясно можем понять, что определение функции — это зависимость одной переменной от другой.
Очень важно понимать, что y = 80 * x не единственная зависимость. Стоит нам лишь изменить скорость автомобиля, то все ý при тех же значениях аргумента будут совсем другие. Кроме того, существует огромное множество зависимостей, которые могут иметь другой вид.
Способы задания
Всего в математике существует три способа задания функции:
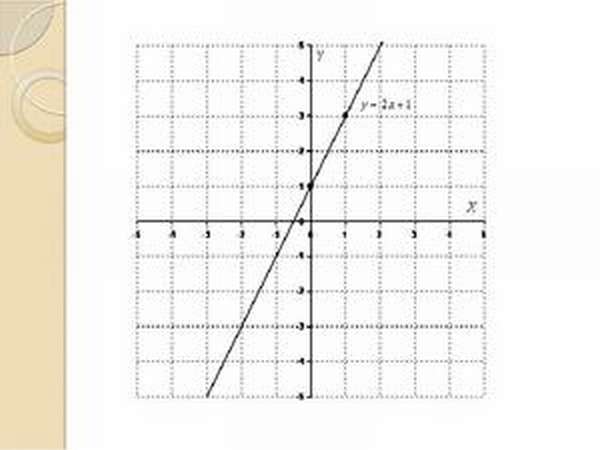
Перед вами координатная плоскость — основа для графика. Она состоит из вертикальной оси Y оси значений, и из горизонтальной оси X аргумента. У координатной плоскости обязательно есть начало отсчёта, которая обозначается нулём, и единичный отрезок (в данном примере единичный отрезок равен одной клетке).
На координатной плоскости мы можем взять любой единичный отрезок. Например, если нам удобно, значение одной клетки будет ни 1, а 100. Следовательно, две клетки 200 и так далее. Здесь мы можем построить любой график и, соответственно, увидеть любую зависимость.
Свойства
В алгебре есть невообразимое количество свойств функции, но основными и действительно важными являются лишь некоторые.
Подводя итог, мы можем сказать, что функция — это важнейшее понятие в математике, ведь, по сути, ею можно описать любые процессы.