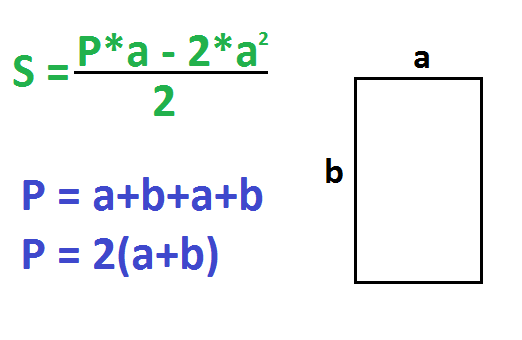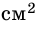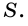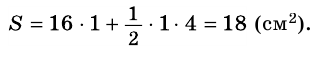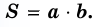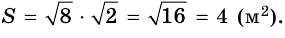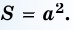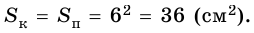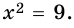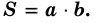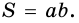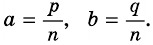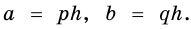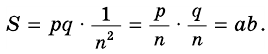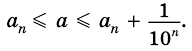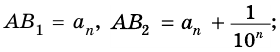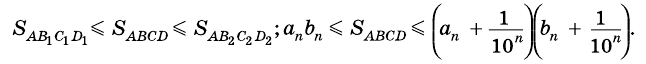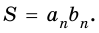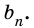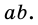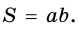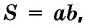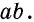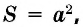Площадь прямоугольника что это такое

Как найти площадь прямоугольника – 9 способов с формулами и примерами

Самый простой способ – перемножить две стороны. Но иногда эти две стороны неизвестны.

Умножьте его ширину на высоту. Это самый простой способ найти площадь прямоугольника. Например, если ширина прямоугольника равна 4 см, а высота – 2 см, то площадь будет равна 4*2 = 8 см.

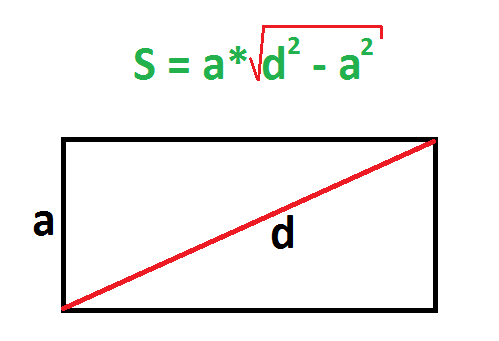
По диагонали и стороне

Должна быть известна диагональ и любая из сторон. Действия:

Пример. Сторона прямоугольника равна 3 см, а диагональ – 5 см. Найдите площадь.

Диагональ в прямоугольнике – это гипотенуза, потому что она всегда находится напротив угла в 90 градусов. Найти диагональ можно по формуле нахождения гипотенузы, например, поделив катет угла A на синус угла A.

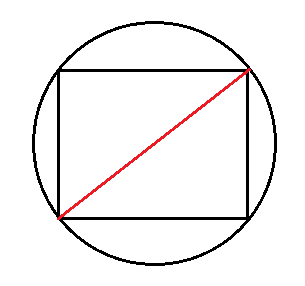
По стороне и диаметру описанной окружности

Вокруг любого прямоугольника можно описать окружность. Вам надо знать диаметр этой окружности и любую из сторон прямоугольника.

Пример. Найдите площадь прямоугольника, если диаметр описанной окружности равен 10 см, а одна из сторон равна 8 см.

Диаметр описанной окружности всегда равен диагонали прямоугольника. Смотрите:

А найти диагональ можно по формуле гипотенузы прямоугольного треугольника.

Диаметр равен двум радиусам, потому что радиус – это половина диаметра.

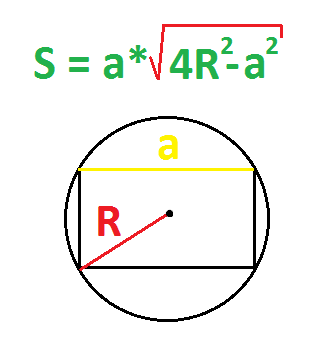
По радиусу описанной окружности и стороне

Можно просто найти диаметр (умножить радиус на два) и использовать формулу выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 5 см, а одна из сторон равна 6 см.

Радиус = половине диаметра.

Радиус = половине гипотенузы прямоугольного треугольника, вокруг которого описана окружность. Потому что эта гипотенуза = диагонали прямоугольника = диаметру.

По стороне и периметру – 1 способ

Периметр – это сумма всех сторон прямоугольника. P=a+b+a+b. Другая формула периметра: P=2(a+b).

Если известен периметр и одна сторона, надо найти вторую сторону и перемножить их.

Пример. Периметр прямоугольника равен 14 см, а одна из сторон равна 3 см. Найдите площадь.

По стороне и периметру – 2 способ

Пример. Сторона прямоугольника равна 8, а периметр равен 28. Найдите площадь.

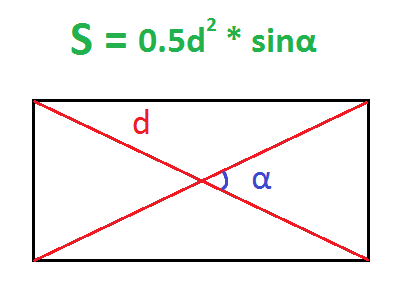
По диагонали и углу между диагоналями

Диагонали прямоугольника всегда равны.

Пример. Найдите площадь прямоугольника, диагональ которого равна 10 см, а угол между диагоналями – 30 градусов.

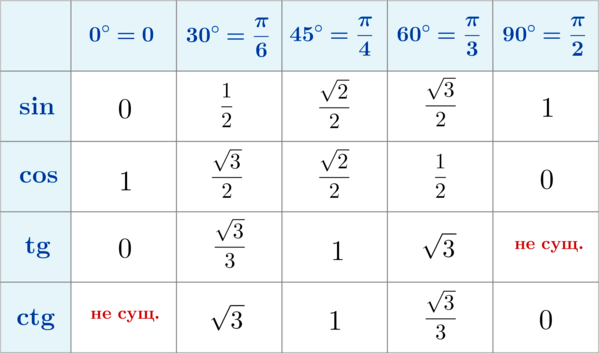
Вот еще вам таблица основных значений из тригонометрии. Там как раз отмечено, что синус 30 градусов всегда равен 0,5 (1/2).

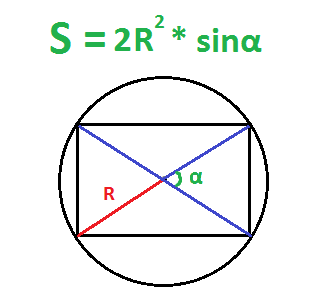
По радиусу описанной окружности и углу между диагоналями – первый способ

Радиус описанной окружности равен половине ее диаметра, а диаметр равен диагонали прямоугольника. Надо найти диаметр и посчитать площадь по формуле выше.

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6 см, а угол между диагоналями – 30 градусов.

По радиусу описанной окружности и углу между диагоналями – второй способ

Пример. Найдите площадь прямоугольника, если радиус описанной окружности равен 6, а угол между диагоналями – 30 градусов.

Покритикуйте статью и стиль подачи материала в комментариях, я внесу правки. Это моя вторая статья по математике, я хочу, чтобы они все были образцовыми.

Источник

Содержание:

Любой многоугольник ограничивает некоторую часть плоскости. Эту часть плоскости называют внутренней областью многоугольника. На рисунке 226 внутренняя область многоугольника закрашена. Будем рассматривать многоугольник вместе с его внутренней областью.

Определение площади прямоугольника

Сформулируем основные свойства площади:

Например, если за единицу измерения длины взять 1 см, то соответствующей единицей измерения площади будет площадь квадрата со стороной 1 см. Такой квадрат имеет площадь 1

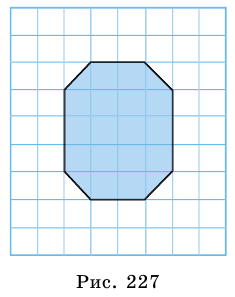
Площадь фигуры принято обозначать буквой

Пример:

Найдите площадь многоугольника, изображенного на рисунке 227, если сторона клетки равна 1 см.

Решение:

Внутренняя область многоугольника состоит из шестнадцати клеток со стороной 1 см, площадь каждой из которых 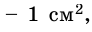и четырех треугольников, площадь каждого из которых равна половине площади клетки. Следовательно, площадь фигуры

Ответ. 18

Площади некоторых фигур можно находить по формулам. Например, из курса математики предыдущих классов нам известны формулы для вычисления площадей прямоугольника, квадрата, круга.

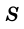
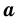
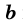
Теорема (о площади прямоугольника). Площадь прямоугольника со сторонами и вычисляется по формуле

Доказательство этой теоремы достаточно громоздко, ознакомиться с ним можно в Приложении 2 (с. 194).

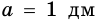
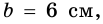
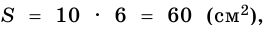
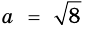
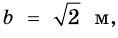
Если стороны прямоугольника и тогда а если и то

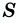
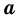
Следствие. Площадь квадрата со стороной вычисляется по формуле

Пример:

Квадрат и прямоугольник имеют равные площади. Сторона квадрата равна 6 см, а одна из сторон прямоугольника в 4 раза больше другой. Найдите периметр прямоугольника.

Решение:

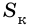
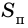
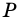
Пусть — площадь квадрата, — площадь прямоугольника, — периметр прямоугольника.

1)

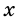
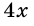
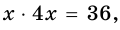
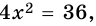
2) Пусть одна из сторон прямоугольника равна см, тогда вторая равна см. По формуле площади прямоугольника имеем уравнение:

то есть откуда

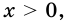
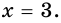
Учитывая, что имеем: Следовательно, стороны прямоугольника равны 3 см и 4 • 3 = 12 (см).

3) (см).

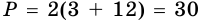
Геометрические знания, связанные с измерением площади, берут свое начало в глубине тысячелетий.

Еще за 2-3 тысячи лет до н. э. вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. Эталоном при измерении площадей им служил квадрат со стороной, равной единице длины.

Древние египтяне 4000 лет назад для измерения площади прямоугольника, треугольника и трапеции уже пользовались теми же формулами, что и мы сейчас.

В своих «Началах» Евклид не употреблял слово «площадь», так как он уже под самим словом «фигура» понимал часть плоскости, ограниченную той или иной замкнутой линей, т. е. площадь. Евклид не выражал результат измерения площади числом, а сравнивал площади разных фигур между собой, употребляя слово «равновеликие». Как, например, в Задаче 16 из первой книги «Начал»: «Параллелограммы, находящиеся на равных основаниях и между теми же параллельными, равны между собой, т. е. равновелики. Докажите!».

Как и другие ученые древности, Евклид занимался вопросами превращения одних фигур в другие, им равновеликие. Так, в «Началах» решалась задача о построении квадрата, равновеликого любому данному многоугольнику.

Теорема о площади прямоугольника

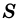
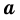
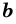
Теорема (о площади прямоугольника). Площадь прямоугольника со сторонами и вычисляется по формуле

Доказательство:

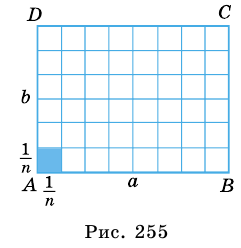
Пусть — произвольный прямоугольник, у которого (рис. 255). Докажем, что

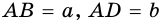
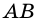
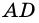
1) Если длины отрезков и являются рациональными числами

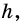
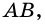
(целыми или дробными), то существует отрезок такой длины которую можно отложить целое число раз и на отрезке и на отрезке

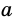
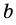
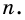
Приведем числа и к общему знаменателю Получим:

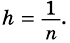
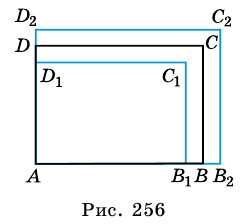
Тогда Имеем

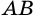
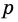
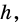
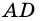
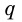
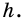
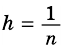
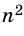
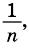
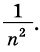
Разобьем отрезок на равных частей длиной a — на равных частей длиной Через точки деления проведем прямые, параллельные сторонам прямоугольника (рис. 255). Эти прямые разобьют весь прямоугольник на pq равных квадратов со стороной (один из таких квадратов закрашен на рисунке 255). Так как единичный квадрат вмещает ровно квадратов со стороной то площадь одного квадрата с такой стороной равна Площадь прямоугольника равна сумме площадей всех квадратов. Имеем:

2) Рассмотрим случай, когда хоть одна из длин отрезков или является числом иррациональным (бесконечной десятичной дробью).

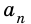
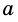
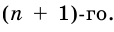
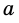
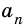
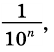
Пусть число получили из числа отбрасыванием всех десятичных знаков после запятой, начиная с Так как отличается от не более чем на то

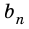
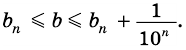
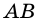
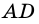
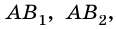
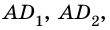
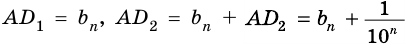
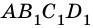
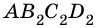
Аналогично рассмотрим число такое, что На прямых

и отложим отрезки где

и построим прямоугольники и (рис. 256).

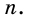
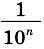
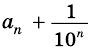
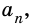
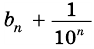
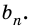
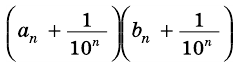
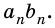
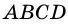
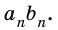
Будем неограниченно увеличивать число Тогда число станет очень малым, а потому число практически не будет отличаться от числа а число практически не будет отличаться от числа Поэтому произведение практически не будет отличаться от произведения Следовательно, из последнего двойного неравенства следует, что площадь прямоугольника практически не отличается от числа Поэтому

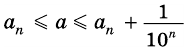
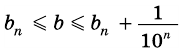
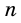
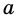
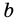
Но из неравенств и при неограниченном увеличении числа следует, что число практично не отличается от числа а число — от числа

Следовательно, число 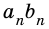практически не отличается от числа

Окончательно имеем:

Площадь прямоугольника с доказательством

Самой простой фигурой с точки зрения вычисления площади является прямоугольник.

Теорема (формула площади прямоугольника)

Площадь прямоугольника равна произведению его соседних сторон:

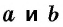
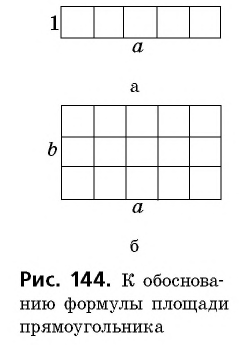
где — стороны прямоугольника.

Приведем рассуждения, на которых основывается доказательство этой теоремы.

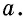
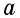
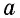
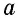
Сначала необходимо рассмотреть прямоугольник со сторонами 1 и Поскольку в отрезке единица измерения длины укладывается раз, то в этом прямоугольнике единица измерения площади (единичный квадрат) будет укладываться также раз (рис. 144, а), т.е. площадь этого прямоугольника равна

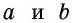
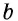
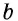
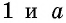
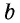
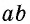
В общем случае для прямоугольника со сторонами рассуждаем так: поскольку в отрезке единица измерения длины укладывается раз, то прямоугольник со сторонами будет укладываться в данном прямоугольнике также раз (рис. 144, б). Тогда единица измерения площади укладывается в данном прямоугольнике раз, т.е. площадь прямоугольника равна

Полное доказательство этой теоремы приводится в Приложении 1.

Следствие (формула площади квадрата)

Площадь квадрата равна квадрату его стороны:

где 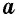— сторона квадрата.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник