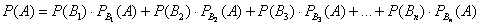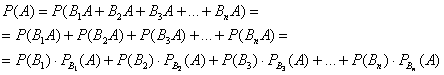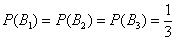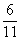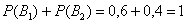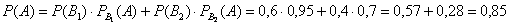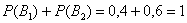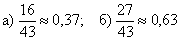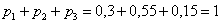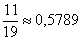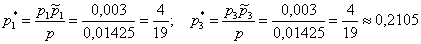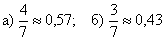Что такое система гипотез в теории вероятностей
Формула полной вероятности. Вероятность гипотез
Формула полной вероятности. Вероятность гипотез
Формула полной вероятности. Вероятность гипотез
Формула полной вероятности
Вероятность гипотез. Формула Байеса
Для этого используем теорему умножения.
$P(AB_1)=P(A)\cdot P_A(B_1)=P(B_1)\cdot P_ < B_ < 1 >> (A)$
$P_A ( < B_1 >)=\frac < P( < B_1 >)\cdot P_ < B_1 >( A ) > < P( A ) >$, Формула Байеса
Сделаем два предположения, две гипотезы:
Далее:
Функции k-значной логики. Элементарные функции. Лемма об аналоге правила де Моргана
Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных
Теорема о предполных классах
Гармонические поля
Вычисление двойного интеграла. Двукратный интеграл
Теорема об аналоге СДНФ в Pk
Вычисление объёмов
Соленоидальное векторное поле
Механические приложения тройного интеграла
Теорема Остроградского
СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице
Дифференциальные характеристики векторного поля
Вычисление площади поверхности
Определение тройного интеграла. Теорема существования тройного интеграла
Приложение 5. Гипотезы и их вероятности. Формула полной вероятности. Формула Байеса
Среди альтернатив, предлагаемых критиками подхода NHST (статистической проверки нулевой гипотезы) имеется так называемый байесовский подход. Он опирается на формулу Байеса, которую мы далее выведем и обсудим. Мы не являемся сторонниками этой альтернативы, однако считаем, что общее представление об этом подходе может быть полезно читателю.
П5.1. Условная вероятность. Формула полной вероятности
Пример 5.1(1). Предположим, что у нас имеется две одинаковые корзины. В одной содержится 8 белых и 2 черных шара, а в другой — 1 белый и 5 черных шаров. Процедура выбора шара проводится в два этапа. Сначала случайно выбирается одна из двух одинаковых корзин, затем из выбранной корзины наугад вынимается шар. Нас интересуют два вопроса:
1) Какова вероятность того, что вынутый по такой процедуре шар будет белым?
2) Если первый шар оказался белым, то какова вероятность того, что вытянутый наугад из той же корзины следующий шар будет белым?
Обсудим сначала второй вопрос. Интуитивно понятно, что результат «вытянут белый шар» может быть интерпретирован как аргумент в пользу того, что на первом этапе процедуры скорее всего была выбрана корзина номер 1, с бóльшим количеством белых шаров. Эта интуиция может быть переведена в точные значения вероятностей с помощью так называемой формулы Байеса. После расчета соответствующих вероятностей ответ на второй вопрос будет достаточно легко дать.
Обозначим символом W событие «Достать белый шар из корзины, выбранной наугад из двух описанных корзин». Оно может наступить только вместе с одним из попарно несовместимых событий \( H_1 \) и \( H_2 \) (будем называть их гипотезами: «Выбрать первую корзину» и «Выбрать вторую корзину»).
Для доказательства в общем случае мы будем использовать так называемую геометрическую интерпретацию вероятностей (рис. П5.1(2)). Внешний овал Ω изображает пространство всех возможных исходов. В испытании может появиться любой из них (одна точка внутри овала), причем все с равными вероятностями. Тогда вероятность наступления сложного события W равна отношению «количества» точек внутри W к «количеству» точек во внешнем овале Ω, точнее говоря, отношению площадей W и Ω. Если положить площадь Ω равной единице, то вероятности всех событий, изображенных фигурами на рисунке, будет равна их площадям.
Вероятность наступления W будет выражаться в таком случае формулой \( P(W)=P(WH_1)+P(WH_2) \) .
Если обозначить \( P(W|H_1) \) условную вероятность вытянуть белый шар, если на первом шаге была выбрана первая корзина, то вероятность \( P(WH_1) \) можно представить в виде произведения \( P(W|H_1)P(H_1) \) . Действительно, \( P(WH_1) \) это доля площади левой, заштрихованной стороны внутреннего овала на рис. П5.1(2), по отношению к площади внешнего овала, представляющего собой полную систему событий Ω. Отношение площадей \( P(WH_1)/P(\Omega) \) можно преобразовать в вид,
Первая дробь представляет собой \( P(W|H_1) \) — долю площади \( WH_1 \) в \( H_1 \) , а вторая по аналогичным соображениям \( P(H_1) \) (долю площади \( H_1 \) в Ω).
Таким образом, \( P(WH_1)=P(W|H_1)P(H_1) \) .
Произведя теперь подстановку, получаем формулу
которая и представляет собой формулу полной вероятности для случая двух слагаемых. Если гипотез больше, то и сумма становится длиннее. В общем случае она такова:
Первая задача нашего примера решается так: с вероятностью 1/2 мы выбираем первую корзину, из которой белый шар достается с вероятностью 8/10; с вероятностью 1/2 вторую корзину, из которой белый шар достается с вероятностью 1/6. Общая вероятность вытянуть белый шар равна
Теперь перейдем ко второму вопросу: если первый шар оказался белым, то какова вероятность того, что вытянутый наугад из той же корзины следующий шар будет белым?
П5.2. Формула Байеса
Для того чтобы на него ответить, надо рассчитать вероятности того, что у нас в руках первая или вторая корзина, при условии, что мы достали из этой имеющейся в руках корзины белый шар, а затем применить формулу полной вероятности для новых вероятностей гипотез.
Заметим, что \( P(WH_1) \) может быть вычислена двумя симметричными способами \( P(WH_1)=P(H_1 |W)P(W) \) и \( P(WH_1)=P(W|H_1)P(H_1). \) Если мы приравняем правые части обоих равенств, то получим \( P(H_1│W)P(W)=P(W|H_1)P(H_1) \) откуда
Эта формула и называется формулой Байеса. Мы теперь можем ответить на вопрос о вероятности вынуть белый шар повторно. Учитывая, что ранее мы нашли \( P(W)=\frac<29> <60>\) , по формуле Байеса рассчитываем: после обнаружения, что вынутый первый шар — белый, вероятность того, что у нас в руках первая корзина равна
Не приходится сомневаться, что вероятность того, что в руках у нас вторая корзина, равна \( 1-\frac<24><29>=\frac<5> <29>\) .
Теперь вероятность достать белый шар из первой корзины равна 7/9, поскольку один белый шар из корзины уже достали. Из второй корзины достать белый шар уже невозможно. Подставляя в формулу полной вероятности новые вероятности, получаем
П5.3. Геометрическая интерпретация формулы полной вероятности и формулы Байеса
Формула Байеса имеет другую форму, которая делает понятным механизм вычисления условной вероятности гипотезы. Мы опять будем разбирать ее на примере с двумя гипотезами. Если учесть, что
и заменить P(W) в знаменателе формулы Байеса на правую часть этой формулы (вспомним, что по ней мы и рассчитывали P(W)), то мы получим второй общеупотребительный вариант формулы Байеса
Заменим теперь обратно произведение \( P(W|H_1)P(H_1) \) на \( P(WH_1) \) , а произведение \( P(W|H_2)P(H_2) \) на \( P(WH_2) \) . Формула тогда примет вид
Эта формула легко интерпретируется с помощью рис. П5.1(2). Если произошло событие W, то это значит, что случилось одно из элементарных событий, изображаемых внутренним овалом. Вероятность того, что происшедшее элементарное событие представляло правую, бóльшую часть внутреннего овала, равна доле площади этой части в площади всего внутреннего овала, что и выражается последней нашей формулой
В заключение параграфа дадим вторую форму формулы Байеса в общем случае:
Ее интерпретация совершенно аналогична приведенной выше интерпретации частного случая. Вся дробь равна доле слагаемого, помещенного в числитель, во всей сумме, стоящей в знаменателе.
Во многих практических случаях формула Байеса работает совершенно адекватно. Полученные вероятности могут проверяться статистически и выдерживают такую проверку. Т.е. если мы будем проводить многократно испытания по выниманию шаров из двух корзин, как это задано в примере, и фиксировать из них только случаи, когда первый вынутый шар был белым, и смотреть долю случаев, когда этот исход наблюдался в случае выбора первой корзины, то частота будет приближаться к вычисленной по формуле Байеса вероятности \( P(H_1|W) \) .
П5.4. Обобщение байесовского подхода
Пока речь у нас шла о «гипотезах», довольно скромных и вполне определенных. Их специфика состоит в том, что они выразимы на языке элементарных событий, т.е. сами являются законными событиями.
Однако байесовская схема кажется некоторым исследователям приложимой и в контексте научных исследований, поскольку, как они надеются, с ее помощью можно пересчитывать вероятности теоретических гипотез после единичного наблюдения. Действие экспериментальной выборки на вероятности гипотез можно свести к последовательному пересчету по каждому испытуемому, т.е., сначала пересчитать вероятности по результатам первого испытуемого, потом полученные вероятности гипотез пересчитать по результатам второго испытуемого и т.д. до исчерпания всего набора испытуемых. Можно доказать, что итог не будет зависеть от порядка испытуемых, если только все их результаты будут использованы.
В научных исследованиях мы ведь могли бы и ограничиться вероятностями гипотез, вместо принятия той или иной гипотезы в качестве окончательно истинной. Это могло бы звучать, например, так: «в настоящее время мы считаем, что пара теорий “динамика Ньютона” и “общая теория относительности Эйнштейна” делят единичную вероятность в соотношении \( \frac<1> <100>\) против \( \frac<99> <100>\) . В зависимости от результатов назначенного на завтра эксперимента на синхрофазотроне в Дубне, эти вероятности будут пересчитаны».
Примем, однако, во внимание, следующую вещь. В примере 5.1(1) мы рассчитали вероятность того, что у нас в руках первая корзина, при условии, что извлеченный из этой корзины шар был белым. В условиях задачи было указано, что вероятности взять в руки первую и вторую корзины исходно равны 1/2. Расчет проводился по формуле
Если бы вероятности были другие, например \( P(«взять\spaceв\spaceруки\spaceпервую\spaceкорзину»)=1/3 \) ; \( P(«взять\spaceв\spaceруки\spaceвторую\spaceкорзину»)=2/3 \) , то итоговая вероятность (при условии извлечения белого шара из взятой в руки корзины) также была бы другой, а именно
Разные априорные (до-опытные) вероятности приводят к разным результатам пересчета по Байесу.
Вопрос, стало быть, состоит в том, что еще до всякого исследования мы должны иметь некоторые априорные вероятности наших гипотез, чтобы с помощью эмпирических проверок получать какие-то новые вероятности гипотез.
Мы можем сформулировать теперь принципиальное утверждение: Если перед исследованием не сделано никаких предположений об априорных вероятностях противопоставленных друг другу гипотез, то и после получения любых эмпирических результатов невозможно делать выводы об апостериорных вероятностях этих гипотез. Неразрешимая проблема байесовского подхода лежит здесь: эти априорные вероятности нам взять неоткуда. Например, какова априорная вероятность того, что есть телепатия? Этот вопрос надо решить прежде, чем мы вознамеримся использовать байесовский подход для ориентированного на статистику доказательства ее существования. Впрочем, наше возражение касается не только байесовских выводов, но и любых других эмпирических проверок таких теорий.
П5.5. Методологическое замечание
Гипотезы, о которых шла речь в примере, как мы говорили, существенно отличаются от теоретических гипотез. Мы вполне можем организовать ситуацию так, что вероятность взять в руки первую из предложенных корзин реально будет равна 1/2. И мы можем повторять экспериментирование с этими равновероятно оказывающимися в руках корзинами и убедиться, что к пересчитанным по формуле Байеса вероятностям сходятся эмпирические частоты. Но вероятности теоретических гипотез принадлежат другому уровню. Даже проделывая осмысленную работу по байесовскому уточнению каким-то разумным образом заданных априорных вероятностей теоретических гипотез, мы никогда не сможем сконструировать метод проверки, в котором какие-то эмпирические частоты сходились бы к этим вероятностям. Такие вероятности обычно называют субъективными. При их использовании надо иметь в виду существенное отличие от вероятностей, о которых говорит математическая теория вероятностей. Последняя говорит о вероятностях возможных событий, а первая о вероятностях истинности утверждений о возможных событиях, что является существенно более сложным предметом, как только мы выходим за пределы утверждений о совокупностях элементарных событий. Таким образом, байесовский подход не способен полноценно заменить подход NHST.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Формула полной вероятности и формулы Байеса
На данном уроке мы рассмотрим важное следствие теорем сложения и умножения вероятностей и научимся решать типовые задачи по теме. Читателям, которые ознакомились со статьёй о зависимых событиях, будет проще, поскольку в ней мы уже по факту начали использовать формулу полной вероятности. Если Вы зашли с поисковика и/или неважно разбираетесь в теории вероятностей (ссылка на 1-й урок курса), то сначала рекомендую посетить указанные страницы.
Собственно, продолжаем. Рассмотрим зависимое событие 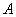
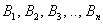
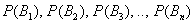
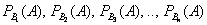
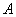
Эта формула получила название формулы полной вероятности. В учебниках она формулируется теоремой, доказательство которой элементарно: согласно алгебре событий, 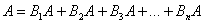
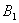
Наверное, многие предчувствуют содержание первого примера =)
Куда ни плюнь – везде урна:
Имеются три одинаковые урны. В первой урне находятся 4 белых и 7 черных шаров, во второй – только белые и в третьей – только черные шары. Наудачу выбирается одна урна и из неё наугад извлекается шар. Какова вероятность того, что этот шар чёрный?
Решение: рассмотрим событие 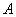
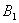
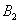
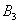
Так как урна выбирается наугад, то выбор любой из трёх урн равновозможен, следовательно:
Обратите внимание, что перечисленные гипотезы образуют полную группу событий, то есть, по условию чёрный шар может появиться только из этих урн, а например, не прилететь с бильярдного стола. Проведём простую промежуточную проверку: 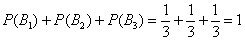
В первой урне 4 белых + 7 черных = 11 шаров, по классическому определению:
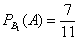
Во второй урне только белые шары, поэтому в случае её выбора появление чёрного шара становится невозможным: 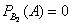
И, наконец, в третьей урне одни чёрные шары, а значит, соответствующая условная вероятность извлечения чёрного шара составит 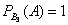
По формуле полной вероятности: 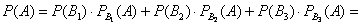
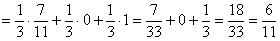
Ответ:
Разобранный пример снова наводит на мысль о том, как важно ВНИКАТЬ В УСЛОВИЕ. Возьмём те же задачи с урнами и шарами – при их внешней схожести способы решения могут быть совершенно разными: где-то требуется применить только классическое определение вероятности, где-то события независимы, где-то зависимы, а где-то речь о гипотезах. При этом не существует чёткого формального критерия для выбора пути решения – над ним почти всегда нужно думать. Как повысить свою квалификацию? Решаем, решаем и ещё раз решаем!
В тире имеются 5 различных по точности боя винтовок. Вероятности попадания в мишень для данного стрелка соответственно равны 0,5; 0,55; 0,7; 0,75 и 0,4. Чему равна вероятность попадания в мишень, если стрелок делает один выстрел из случайно выбранной винтовки?
Краткое решение и ответ в конце урока.
В большинстве тематических задач гипотезы, конечно же, не равновероятны:
В пирамиде 5 винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок производит один выстрел из наудачу взятой винтовки.
Решение: в этой задаче количество винтовок точно такое же, как и в предыдущей, но вот гипотезы всего две:
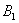
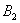
По классическому определению вероятности: 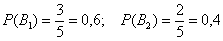
Контроль:
Рассмотрим событие: 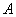
По условию: 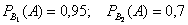
По формуле полной вероятности:
Ответ: 0,85
На практике вполне допустим укороченный способ оформления задачи, который вам тоже хорошо знаком:
Решение: по классическому определению: 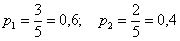
По условию, 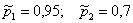
По формуле полной вероятности:
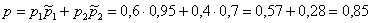
Ответ: 0,85
Следующая задача для самостоятельного решения:
Двигатель работает в трёх режимах: нормальном, форсированном и на холостом ходу. В режиме холостого хода вероятность его выхода из строя равна 0,05, при нормальном режиме работы – 0,1, а при форсированном – 0,7. 70% времени двигатель работает в нормальном режиме, а 20% – в форсированном. Какова вероятность выхода из строя двигателя во время работы?
На всякий случай напомню – чтобы получить значения вероятностей проценты нужно разделить на 100. Будьте очень внимательны! По моим наблюдениям, условия задач на формулу полной вероятности частенько пытаются подзапутать; и я специально подобрал такой пример. Скажу по секрету – сам чуть не запутался =)
Решение в конце урока (оформлено коротким способом)
Задачи на формулы Байеса
Материал тесно связан с содержанием предыдущего параграфа. Пусть событие 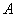
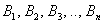
При условии, что событие 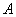
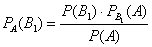
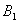
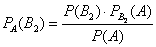
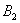
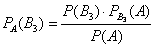
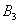
…
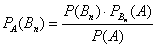
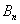
На первый взгляд кажется полной нелепицей – зачем пересчитывать вероятности гипотез, если они и так известны? Но на самом деле разница есть:
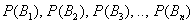
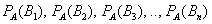
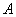
Рассмотрим это различие на конкретном примере:
На склад поступило 2 партии изделий: первая – 4000 штук, вторая – 6000 штук. Средний процент нестандартных изделий в первой партии составляет 20%, а во второй – 10%. Наудачу взятое со склада изделие оказалось стандартным. Найти вероятность того, что оно: а) из первой партии, б) из второй партии.
Первая часть решения состоит в использовании формулы полной вероятности. Иными словами, вычисления проводятся в предположении, что испытание ещё не произведено и событие «изделие оказалось стандартным» пока не наступило.
Рассмотрим две гипотезы:
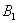
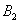
Всего: 4000 + 6000 = 10000 изделий на складе. По классическому определению: 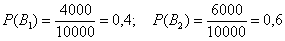
Контроль:
Рассмотрим зависимое событие: 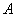
В первой партии 100% – 20% = 80% стандартных изделий, поэтому: 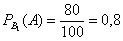
Аналогично, во второй партии 100% – 10% = 90% стандартных изделий и 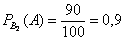
По формуле полной вероятности:
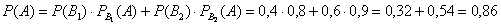
Часть вторая. Пусть наудачу взятое со склада изделие оказалось стандартным. Эта фраза прямо прописана в условии, и она констатирует тот факт, что событие 
По формулам Байеса:
а) 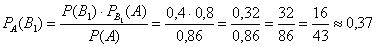
б) 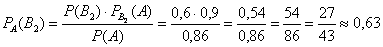
После переоценки гипотезы 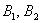
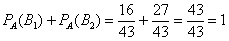
Ответ:
Понять смысл переоценки гипотез нам поможет Иван Васильевич, которой снова сменил профессию и стал директором завода. Он знает, что сегодня 1-й цех отгрузил на склад 4000, а 2-й цех – 6000 изделий, и приходит удостовериться в этом. Предположим, вся продукция однотипна и находится в одном контейнере. Естественно, Иван Васильевич предварительно подсчитал, что изделие, которое он сейчас извлечёт для проверки, с вероятностью 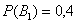
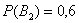
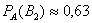
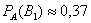
Вы скажете, чистый субъективизм? Отчасти – да, более того, сам Байес интерпретировал апостериорные вероятности как уровень доверия. Однако не всё так просто – в байесовском подходе есть и объективное зерно. Ведь вероятности того, что изделие будет стандартным (0,8 и 0,9 для 1-го и 2-го цехов соответственно) это предварительные (априорные) и средние оценки. Но, выражаясь философски – всё течёт, всё меняется, и вероятности в том числе. Вполне возможно, что на момент исследования более успешный 2-й цех повысил процент выпуска стандартных изделий (и/или 1-й цех снизил), и если проверить бОльшее количество либо все 10 тысяч изделий на складе, то переоцененные значения 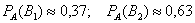
Кстати, если Иван Васильевич извлечёт нестандартную деталь, то наоборот – он будет больше «подозревать» 1-й цех и меньше – второй. Предлагаю убедиться в этом самостоятельно:
На склад поступило 2 партии изделий: первая – 4000 штук, вторая – 6000 штук. Средний процент нестандартных изделий в первой партии 20%, во второй – 10%. Наудачу взятое со склада изделие оказалось нестандартным. Найти вероятность того, что оно: а) из первой партии, б) из второй партии.
Условие отличатся двумя буквами, которые я выделил жирным шрифтом. Задачу можно решить с «чистого листа», или воспользоваться результатами предыдущих вычислений. В образце я провёл полное решение, но чтобы не возникло формальной накладки с Задачей №5, событие «наудачу взятое со склада изделие будет нестандартным» обозначено через 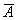
Байесовская схема переоценки вероятностей встречается повсеместно, причём её активно эксплуатируют и различного рода мошенники. Рассмотрим ставшее нарицательным АО на три буквы, которое привлекает вклады населения, якобы куда-то их инвестирует, исправно выплачивает дивиденды и т.д. Что происходит? Проходит день за днём, месяц за месяцем и всё новые и новые факты, донесённые путём рекламы и «сарафанным радио», только повышают уровень доверия к финансовой пирамиде (апостериорная байесовская переоценка в связи с произошедшими событиями!). То есть, в глазах вкладчиков происходит постоянное увеличение вероятности того, что «это серьёзная контора»; при этом вероятность противоположной гипотезы («это очередные кидалы»), само собой, уменьшается и уменьшается. Дальнейшее, думаю, понятно. Примечательно, что заработанная репутация даёт организаторам время успешно скрыться от Ивана Васильевича, который остался не только без партии болтов, но и без штанов.
К не менее любопытным примерам мы вернёмся чуть позже, а пока на очереди, пожалуй, самый распространенный случай с тремя гипотезами:
Электролампы изготавливаются на трех заводах. 1-й завод производит 30% общего количества ламп, 2-й – 55%, а 3-й – остальную часть. Продукция 1-го завода содержит 1% бракованных ламп, 2-го – 1,5%, 3-го – 2%. В магазин поступает продукция всех трех заводов. Купленная лампа оказалась с браком. Какова вероятность того, что она произведена 2-м заводом?
Заметьте, что в задачах на формулы Байеса в условии обязательно фигурирует некое произошедшее событие, в данном случае – покупка лампы.
Событий прибавилось, и решение удобнее оформить в «быстром» стиле.
Алгоритм точно такой же: на первом шаге находим вероятность того, что купленная лампа вообще окажется бракованной.
Пользуясь исходными данными, переводим проценты в вероятности:
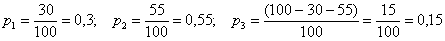
Контроль:
Аналогично: 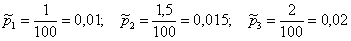
По формуле полной вероятности: 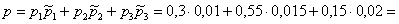
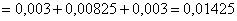
Шаг второй. Пусть купленная лампа оказалась бракованной (событие произошло)
По формуле Байеса:
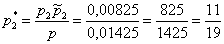
Ответ:
Почему изначальная вероятность 2-й гипотезы 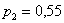
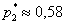
Интересно заметить, что вероятности 1-й и 3-й гипотез, переоценились в ожидаемых направлениях и сравнялись:
Контроль: 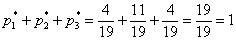
К слову, о заниженных и завышенных оценках:
В студенческой группе 3 человека имеют высокий уровень подготовки, 19 человек – средний и 3 – низкий. Вероятности успешной сдачи экзамена для данных студентов соответственно равны: 0,95; 0,7 и 0,4. Известно, что некоторый студент сдал экзамен. Какова вероятность того, что:
а) он был подготовлен очень хорошо;
б) был подготовлен средне;
в) был подготовлен плохо.
Проведите вычисления и проанализируйте результаты переоценки гипотез.
Задача приближена к реальности и особенно правдоподобна для группы студентов-заочников, где преподаватель практически не знает способностей того или иного студента. При этом результат может послужить причиной довольно-таки неожиданных последствий (особенно это касается экзаменов в 1-м семестре). Если плохо подготовленному студенту посчастливилось с билетом, то преподаватель с большой вероятностью сочтёт его хорошо успевающим или даже сильным студентом, что принесёт неплохие дивиденды в будущем (естественно, нужно «поднимать планку» и поддерживать свой имидж). Если же студент 7 дней и 7 ночей учил, зубрил, повторял, но ему просто не повезло, то дальнейшие события могут развиваться в самом скверном ключе – с многочисленными пересдачами и балансировкой на грани вылета.
Что и говорить, репутация – это важнейший капитал, не случайно многие корпорации носят имена-фамилии своих отцов-основателей, которые руководили делом 100-200 лет назад и прославились своей безупречной репутацией.
Да, байесовский подход в известной степени субъективен, но… так устроена жизнь!
Закрепим материал заключительным индустриальным примером, в котором я расскажу о до сих пор не встречавшихся технических тонкостях решения:
Три цеха завода производят однотипные детали, которые поступают на сборку в общий контейнер. Известно, что первый цех производит в 2 раза больше деталей, чем второй цех, и в 4 раза больше третьего цеха. В первом цехе брак составляет 12%, во втором – 8%, в третьем – 4%. Для контроля из контейнера берется одна деталь. Какова вероятность того, что она окажется бракованной? Какова вероятность того, что извлечённую бракованную деталь выпустил 3-й цех?
Таки Иван Васильевич снова на коне =) Должен же быть у фильма счастливый конец =)
Решение: в отличие от Задач №№5-8 здесь в явном виде задан вопрос, который разрешается с помощью формулы полной вероятности. Но с другой стороны, условие немного «зашифровано», и разгадать этот ребус нам поможет школьный навык составлять простейшие уравнения. За «икс» удобно принять наименьшее значение:
Пусть 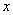
По условию, первый цех производит в 4 раза больше третьего цеха, поэтому доля 1-го цеха составляет 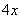
Кроме того, первый цех производит изделий в 2 раза больше, чем второй цех, а значит, доля последнего: 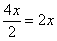
Составим и решим уравнение: 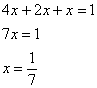
Таким образом: 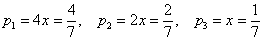
Контроль: 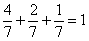
За «икс» изначально можно было принять долю 1-го либо долю 2-го цеха – вероятности выйдут такими же. Но, так или иначе, самый трудный участок пройден, и решение входит в накатанную колею:
Из условия находим:
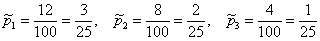
По формуле полной вероятности: 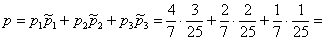
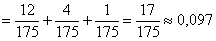
Вопрос второй: какова вероятность 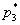
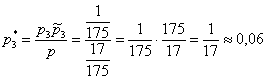
В данном случае пришлось упрощать четырёхэтажную дробь, что в задачах на формулы Байеса приходится делать довольно часто. Но для данного урока я как-то так случайно подобрал примеры, в которых многие вычисления можно провести без обыкновенных дробей.
Коль скоро в условии нет пунктов «а» и «бэ», то ответ лучше снабдить текстовыми комментариями:
Ответ: 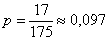
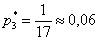
Как видите, задачи на формулу полной вероятности и формулы Байеса достаточно простЫ, и, наверное, по этой причине в них так часто пытаются затруднить условие, о чём я уже упоминал в начале статьи.
Дополнительные примеры есть в файле с готовыми решениями на Ф.П.В. и формулы Байеса, кроме того, наверное, найдутся желающие более глубоко ознакомиться с данной темой в других источниках. А тема действительно очень интересная – чего только стОит один парадокс Байеса, который обосновывает тот житейский совет, что если у человека диагностирована редкая болезнь, то ему имеет смысл провести повторное и даже два повторных независимых обследования. Казалось бы, это делают исключительно от отчаяния… – а вот и нет! Но не будем о грустном.
Задача 2: Решение: рассмотрим гипотезы 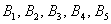
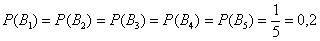
Рассмотрим событие 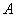
По условию: 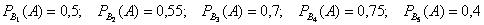
По формуле полной вероятности: 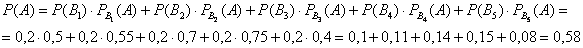
Ответ: 0,58
Задача 4: Решение: из условия находим 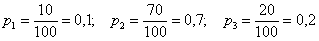
По условию 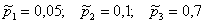
По формуле полной вероятности: 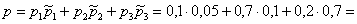
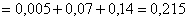
Ответ: 0,215
Задача 6: Решение: рассмотрим две гипотезы:
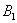
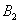
Всего: 4000 + 6000 = 10000 изделий на складе. По классическому определению: 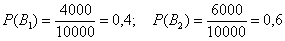
Рассмотрим событие: 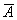
Из условия находим: 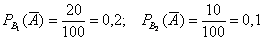
По формуле полной вероятности: 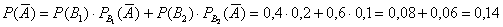
Примечание: данную вероятность легко найти, пользуясь результатом Задачи 5: 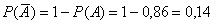
Пусть событие 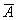
По формулам Байеса:
а) 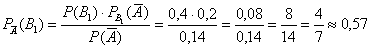
б) 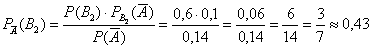
Ответ:
Задача 8: Решение: всего: 3 + 19 + 3 = 25 студентов в группе. По классическому определению:
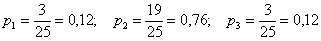
Контроль: 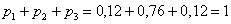
По условию: 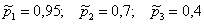
По формуле полной вероятности: 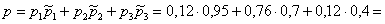
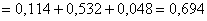
Пусть студент сдал экзамен. По формулам Байеса:
а) 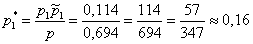
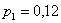
б) 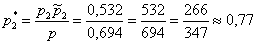
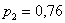
в) 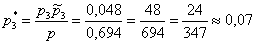
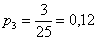
Проверка: 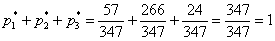
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5