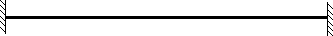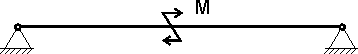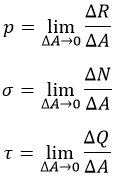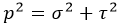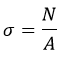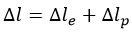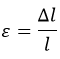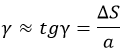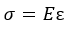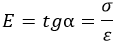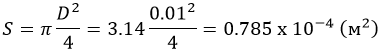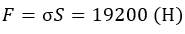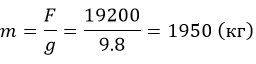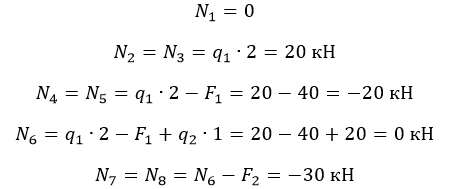Сопромат для чайников с самого начала

18.07.202218.07.2022 admin 0 Comments

Сопромат для чайников с самого начала

Итак, давайте разбираться, зачем понадобилось ломать школьную линейку, оставляя детей без школьных принадлежностей, и чем это может нам помочь. Пришло время добавить к наглядности несколько формул, тут все будет почти так же просто и понятно, как и в первой части сопромата для чайников, но понадобятся знания математики на уровне 4-5 классов и начальные знания по геометрии.

Основы сопромата, расчет прогиба балки

Часто при расчете строительных конструкций важно определить не только геометрические параметры сечения конструкции, но и величину прогиба конструкции с точностью до миллиметра. Дело в том, что величина прогиба для любой конструкции нормируется различными СНиПами и не должна превышать 1/250 для балок междуэтажных перекрытий, 1/200 для чердачных перекрытий и перемычек и так далее, список длинный. Когда расчет производится для себя (например строится частный дом и нужно сделать балки перекрытия или перемычки), то определять величину прогиба не обязательно, никто Вас ругать не будет, главное чтобы по несущей способности расчет был верный, но все же определить прогиб конструкции желательно. Ведь знание величины прогиба позволить более точно выбрать, например, вариант отделки потолка.

Сопромат для чайников

По большому счету основы теории сопротивления материалов (сопромата) даже проще, чем таблица умножения. Таблица умножения большая, ее нужно тупо заучить как «Отче наш», а основы сопромата сводятся к нескольким основным положениям, которые достаточно легко наглядно продемонстрировать и потому их легко запомнить даже абсолютному «чайнику» в сопромате.

Обстоятельства сложились так, что вступительный курс лекций по сопромату я пропустил, так как вернулся после службы на флоте в институт за 2 недели до сессии, поэтому основы сопромата пришлось постигать самому, за что самый суровый и неподкупный препод на потоке, заваливший не одну сотню студентов, поставил мне пятерку. Ну и понеслось, преподаватели, видя пятерку по сопромату, ставить меньшую отметку по своему предмету не решались и в итоге у меня получился красный диплом.

Впрочем не будем отвлекаться, а вернемся к основам в изложении такого же чайника, как и некоторые из вас.

Приведение сосредоточенной нагрузки к эквивалентной равномерно распределенной

Это в свою очередь означает, что расчет нужно вести по разным формулам, например, определять максимальное значение изгибающего момента отдельно для равномерно распределенной нагрузки и отдельно для сосредоточенных нагрузок. То же касается и определения максимального прогиба конструкции. Хорошо, если такая сосредоточенная нагрузка только одна, расчеты при этом не сильно усложнятся, а вот если таких сосредоточенных нагрузок несколько, да еще и приложены они на разных расстояниях друг от друга и несимметрично, то расчет становится достаточно сложным. Между тем, чем больше на строительную конструкцию действует сосредоточенных нагрузок, тем ближе суммарная эпюра моментов от этих сосредоточенных нагрузок к эпюре от равномерно распределенной нагрузки. Поэтому для упрощения расчетов конструкций постоянного по длине сечения вполне допустимо заменять сосредоточенные нагрузки на эквивалентную равномерно распределенную. Однако делать это нужно осторожно, так как варианты приложения сосредоточенных нагрузок бывают разные:

Виды опор, какую расчетную схему выбрать

Основы сопромата. Определение касательных напряжений.

Основы сопромата, момент сопротивления

Расчет на растяжение стержня

Расчет на прочность прямолинейного стержня при действии центрально приложенной растягивающей силы является одной из самых простых задач в теории сопротивления материалов.

Смысл данного расчета сводится к тому, чтобы обеспечить необходимую прочность материала, исходя из условия:

Приведение неравномерно распределенной нагрузки к эквивалентной равномерно распределенной

Иногда при расчете конструкций, на которые действует симметричная распределенная нагрузка, описываемая достаточно сложными уравнениями, возникает необходимость привести данную нагрузку к эквивалентной равномерно распределенной для упрощения этих самых расчетов.

Так например, все мы знаем, что максимальный изгибающий момент при действии равномерно распределенной нагрузки на шарнирно опертую балку будет в середине пролета (l/2) и составит:

Что такое жесткость и гибкость элементов

Разницу в работе гибких и жестких стержней под воздействием нагрузки люди заметили достаточно давно. Так один из мастеров восточных единоборств, гуляя по зимнему саду, сделал примерно следующий вывод: жесткая сухая ветка под тяжестью налипшего снега ломается, а гибкая ветка прогибается и, сбросив налипший снег, возвращается в прежнее положение с минимумом повреждений.

Если перевести это гибкую поэтическую аллегорию, помогавшую мастеру восточных единоборств привлекать новых учеников, на современный жесткий язык теории сопротивления материалов, то звучать это будет примерно так: если напряжения в рассматриваемом поперечном сечении жесткого элемента конструкции превышают значение нормативного сопротивления, то это приведет сначала к значительным пластическим деформациям, а затем, при увеличении напряжений, и к разрушению жесткого элемента (будет это разрушение хрупким или вязким, принципиального значения не имеет). В то же время гибкий элемент конструкции под действием такой же нагрузки, не разрушится, но потеряет устойчивость.

Какой момент инерции выбрать?

В последнее время мне все чаще задают вопрос: какой момент инерции выбрать для расчетов балки и почему? А после этого добавляют примерно следующее: «во всех учебниках сопромата пишут только, что сечение должно стремиться к квадрату, но в жизни часто встречается двутавр, например» или «всюду пишут, что сечение должно стремиться к квадрату и брать надо наименьший момент инерции. Никак не могу ухватить за хвост физический смысл, можно это как-то на пальцах истрактовать?».

Момент силы

Формула для определения момента силы на удивление проста:

Момент инерции, куда пропала скорость?

Статья получилась достаточно большой. Я, хоть и не Толстой Л.Н., но тоже люблю разливаться мыслью по древу, но некоторые моменты все равно оказались упущены или недостаточно акцентированы, что у некоторых, хотя далеко не у всех читалей вызывает вопросы.

Формула прогиба

В статье «Расчетные схемы для балок» задается достаточно много вопросов и делается достаточно много комментариев на тему правильности той или иной формулы. Как правило я отвечаю на вопросы там же в комментариях, но на этот раз тема неординарная и я решил вынести ее в отдельную статью. К тому же в комментариях степень числа можно отобразить только как ^, а это затрудняет восприятие.

Сначала приведу переписку из комментариев касательно правильности формулы прогиба:

Музыкальная теория расчета гибких нитей (Часть 1)

Но если один из родителей еще и разбирается в сопромате, то, увидев столь вольное обращение с гитарой, может ребенка и наказать. Причем очень строго: за грубое нарушение теории расчета гибких нитей. Вот так! Не меньше!

Итак, маленькая теоркомедия в 4 актах.

Акт первый

Мы начинаем прикладывать условно сосредоточенную нагрузку Q к струне в центре тяжести гитары, на расстоянии l/2 от опор.

Источник

Сопромат для чайников — основы, формулы и задачи

Многочисленные учебники «Cопромат для чайников» создают для развенчания мифа о непостижимой сложности дисциплины. Этой наукой пугают на первых курсах вузов. Для начала расшифруем грозный термин «сопротивление материалов».

На деле – проста и решение почти не выходит за рамки школьной задачи о растяжении и сжатии пружины. Другое дело – найти слабое звено конструкции и свести расчет к несложной постановке. Так что не стоит зевать на лекциях по основам механики. При подготовке к урокам можно пользоваться решениями онлайн, но на экзаменах помогут только свои знания.

Что такое сопромат

Это методика расчета деталей, конструкций на способность выдерживать нагрузки в требуемой степени. Или хотя бы для предсказания последствий. Не более, хотя почему-то относят руководство к наукам.

Этой «наукой» прекрасно владели древнегреческие и древнеримские инженеры, сооружавшие сложнейшие механизмы. Понятия не имея о структуре, уравнении состояния вещества и прочих теориях, египтяне строили исполинские плотины и пирамиды.

Основные задачи по сопротивлению материалов

Задача следует напрямую из определения. А вот каковы критерии упомянутого слова «выдерживать»? Неясно, что скрывается под «материалом» и как реальные вещи схематизировать.

Требования

Перечислены далеко не все, но для статики и базовой программы хватит:

Прочность – способность образца воспринимать внешние силы без разрушения. Слегка мнущаяся под весом оборудования подставка никого не интересует. Основную-то функцию она выполняет.

Жесткость – свойство воспринимать нагрузку без существенного нарушения геометрии. Гнущийся под силой резания инструмент даст дополнительную погрешность обработки. К ошибке приведет деформация станины агрегата.

Устойчивость – способность конструкции сохранять стабильность равновесия. Поясним на примере: стержень находится под грузом, будучи прямым – выдерживает, а чуть изогнется – характер напряжения изменится, груз рухнет.

Материал и силы

Как всякая методика, сопромат принимает массу упрощений и прямо неверных допущений:

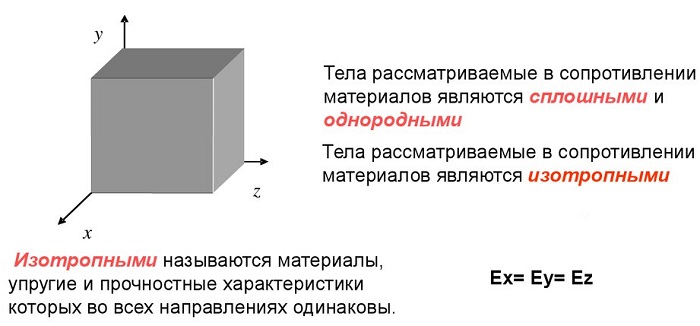
материал однороден, среда сплошная. Внутренние особенности в расчет не берутся;

свойства не зависят от направления;

образец восстанавливает начальные параметры при снятии нагрузки;

поперечные сечения не меняются при деформации;

в удаленных от места нагрузки местах усилие распределяется равно по сечению;

результат воздействия нагрузок равен сумме последствий от каждой;

деформации не влияют на точки приложения сил;

отсутствуют изначальные внутренние напряжения.

Схемы

Служат для создания возможности расчета реальных конструкций:

тело – объект с практически одинаковыми «длина х ширина х высота»;

брус (балка, стержень, вал) – характеризуется значительной длиной.

На рисунке показаны опоры с воспринимаемыми реакциями (обозначены красным цветом):

Рис. 1. Опоры с воспринимаемыми реакциями:

в) жесткая заделка (защемление).

Силы в сопромате

Приложенные извне, уравновешиваются возникающими изнутри. Напомним, рассматривается статическая ситуация. Материал «сопротивляется».

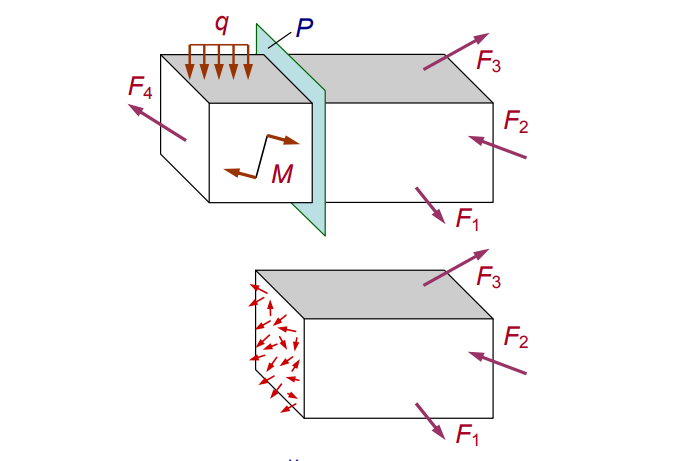
Разделим нагруженное тело виртуальным сечением P (см. рис. 2).

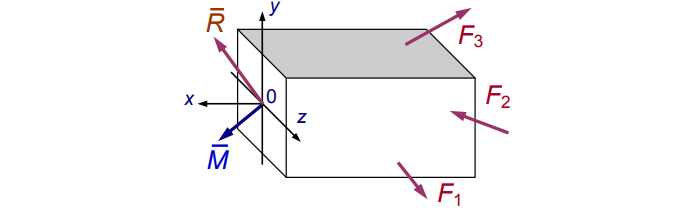
Заменим хаос равнодействующей R и моментом M (см. рис. 3):

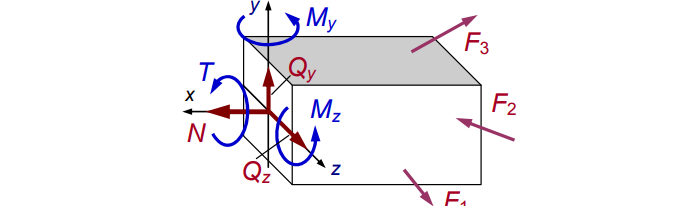
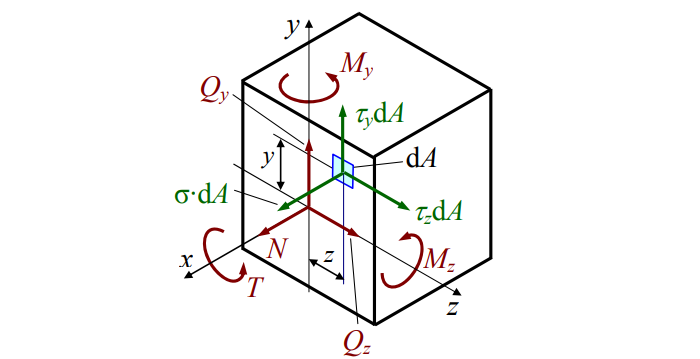
Распределив по осям, получим картину нагрузки сечения (см. рис. 4):

Нагрузки и деформации, изучаемые в сопромате

Изучим несколько принятых терминов.

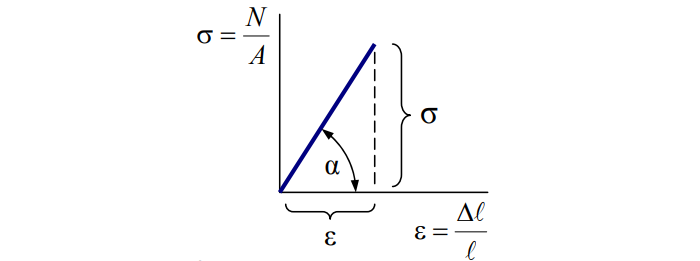
Напряжения

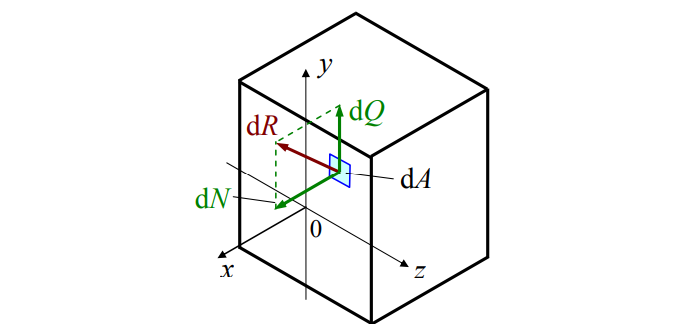
В теле приложенные силы распределяются по сечению. Нагружен каждый элементарный «кусочек». Разложим силы:

Элементарные усилия таковы:

σ – «сигма», нормальное напряжение. Перпендикулярно сечению. Характерно для сжатия / растяжения;

τ – «тау», касательное напряжение. Параллельно сечению. Появляется при кручении;

p – полное напряжение.

Просуммировав элементы, получим:

N – нормальная сила;

A – площадь сечения.

В принятой в России системе СИ сила измеряется в ньютонах (Н). Напряжения – в паскалях (Па). Длины в метрах (м).

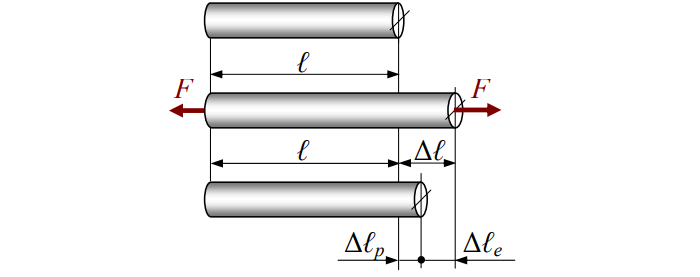
Деформации

Различают деформацию упругую (с индексом «e») и пластическую (с индексом «p»). Первая исчезает по снятии растягивающей / сжимающей силы, вторая – нет.

Полная деформация будет равна:

Деформация относительная обозначается «ε» и рассчитывается так:

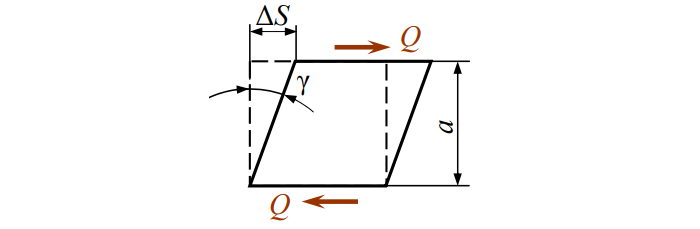
Под «сдвигом» понимается смещение параллельных слоев. Рассмотрим рисунок:

Здесь γ – относительный сдвиг.

Виды нагрузки

Растяжение и сжатие – нагрузка нормальной силой (по оси стержня).

Кручение – действует момент. Обычно рассчитываются передающие усилия валы.

Изгиб – воздействие направлено на искривление.

Основные формулы

Базовый принцип сопромата единственный. В упомянутой задаче о пружине применим закон Гука:

E – модуль упругости (Юнга). Величина зависит от используемого материала. Для стали полагают равным 200 х 10 6 Па.

Сопротивление материала прямо пропорционально деформации:

Закон верен не всегда и не для всех материалов. Как уже упоминалось, принимается как одно из допущений.

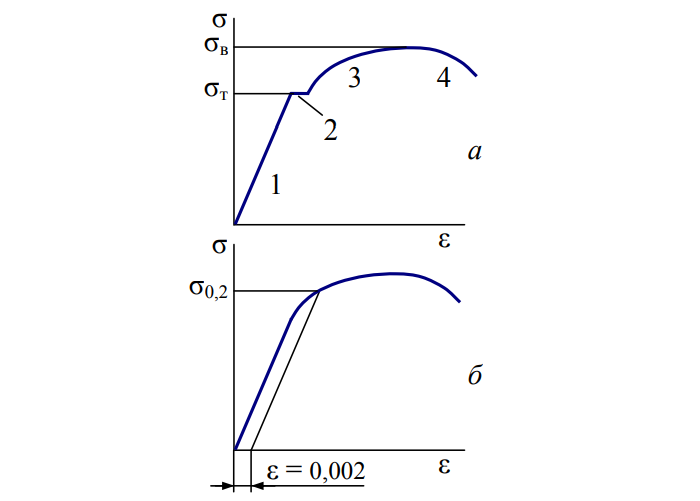
Реальная диаграмма

Растяжение стержня из низкоуглеродистой стали выглядит следующим образом:

График (б) относится к большей части конструкционных материалов: подкаленные стали, сплавы цветных металлов, пластики.

Расчеты обычно ведут по σт (а) и σ0.2 (б). С незначительными пластическими деформациями конструкции или без таковых.

Пример решения задачи

Какой груз допустимо подвесить на пруток из стали 45 Ø10 мм?

σ0,2 для стали 45 равна 245 МПа (из ГОСТ).

Площадь сечения прутка:

Допустимая сила тяжести:

Для получения веса следует разделить на ускорение свободного падения g:

Ответ: необходимо подвесить груз массой 1950 кг.

Как найти опасное сечение

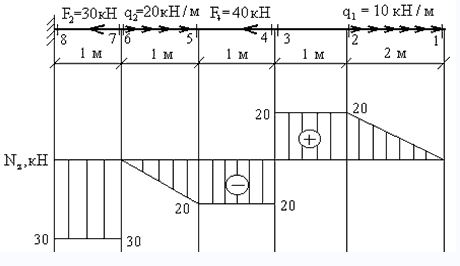
Наиболее простой способ – построение эпюры. На закрепленную балку действуют точечные и распределенные силы. Считаем на характерных участках, начиная с незакрепленного конца.

Усилие положительно, если направлено на растяжение.

На схеме показано, что:

на участке (7 — 8) действует сжатие 30 кН;

на (2 — 3) – растяжение 20 кН.

Зачем и кому нужен сопромат

Даже не имеющий отношения к прочностным расчетам инженер-универсал должен иметь понятие о приблизительных (на 10-20%) значениях. Знать конструкционные материалы, представлять свойства. Чувствовать заранее слабые места агрегатов.

Совершенно необходим разработчикам различных конструкций, машиностроительных изделий. Будущим архитекторам в вузах преподается в виде предмета «Строительная механика».

Методика помогает на стадии проектирования обеспечивать необходимый запас прочности изделий. Стойкость к постоянным и динамичным нагрузкам. Это сберегает массу времени и затрат в дальнейших изготовлении, испытании и эксплуатации изделия. Обеспечивает надежность и долговечность.

Источник

Сопромат для чайников

Впрочем не будем отвлекаться, а вернемся к основам в изложении такого же чайника, как и некоторые из вас.

Если совсем кратко, то основы сопромата, изложенные в данной статье, звучат так:

Вот в принципе и все, далее следуют формулы и прочие расчеты, но попробуем добавить больше наглядности этим положениям на примере балки.

Чтобы наглядно представить себе основы сопромата, достаточно иметь две простых школьных деревянных линейки, например, длиной 20 и 40 см и несколько книг, учебники по сопромату подойдут здесь как нельзя лучше, и стол. Впрочем можно иметь и одну пластмассовую или алюминиевую линейку любой длины и книги любого содержания.

1. Виды опор.

Теперь нужно положить линейку плашмя на два выступа, например на 2 книжки:

Рисунок 1.

Если посмотреть на линейку сбоку, то будет видно не только название учебника, но и то, что линейка лежит плашмя.

1.1. Шарнирные опоры

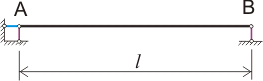
С одной стороны все вроде бы просто, лежит себе линейка на книгах, ну и пусть лежит, а вот если взглянуть на эту ситуацию с точки зрения теоретической механики (до сопромата мы пока еще не добрались), то мы с Вами имеем не обычную школьную линейку, лежащую на книгах, а модель балки на двух скользящих шарнирных опорах и выглядеть это будет так:

Рисунок 2.1

1.2. Горизонтальные линии с косой заштриховкой снизу означают некое устойчивое основание, в данном случае это стол.

1.3. Некоторое расстояние между основанием и опорами балки, обозначенными треугольниками, является неким подобием воздушной подушки и означает, что опоры могут скользить по основанию без трения.

1.4. На самом деле у нашей линейки нет никаких шарниров, связывающих ее с опорами, а опирается линейка, если очень хорошо присмотреться, на выступающие корешки книг и можно изобразить нашу линейку например так:

Рисунок 2.2

В технической литературе такое отображение опор (без шарниров) также встречается и означает, что опоры не препятствуют повороту, но препятствуют перемещению по вертикали и по горизонтали.

1.5. на рисунке 2.1 шарниры находятся на концах балки, на рисунке 2.2 треугольники опор находятся на некотором расстоянии от концов балки. С точки зрения теоретической механики никакой разницы тут нет, если принимать расстояние между опорами и на рисунке 2.1 и на рисунке 2.2 одинаковым, а на концы линейки, находящиеся за пределами опор, ни какая нагрузка не действует.

Расчетная длина балки

1.2. Опорные связи шарнирно закрепленной балки

Любое физическое тело, в данном случае линейка, имеет три степени свободы движения в рассматриваемой плоскости ху: 1) тело может перемещаться вдоль оси х, 2) тело может перемещаться вдоль оси у, 3) тело может вращаться вокруг некоторой точки, даже если свобода перемещения относительно осей х и у ограничена.

Соответственно любая устойчивая и статически определимая конструкция должна иметь как минимум три опорных связи, ограничивающих указанные степени свободы. Балка, показанная на рисунке 2.1, является статически определимой, но не устойчивой, так как у нее только 2 параллельные вертикальные связи. Балка, показанная на рисунке 2.2, является устойчивой, но статически неопределимой, так как у нее 2 вертикальные и две горизонтальные опорные связи. А уравнения статического равновесия позволяют определить только три неизвестных величины (об этом чуть позже).

Поэтому в технической литературе часто встречается следующее отображение шарнирных опор балки:

Рисунок 2.3

Физический смысл такого отображения опорных связей следующий:

2. Эти связи шарнирно соединены не только с балкой но и с неким жестким основанием. А это в свою очередь означает, что не только балка может свободно поворачиваться относительно опорных связей, но и опорные связи могут свободно поворачиваться относительно жесткого основания.

3. Для обеспечения геометрической неизменяемости (устойчивости) системы горизонтальная опорная связь необходима, хотя при расчетах на вертикальную нагрузку она вроде бы и не нужна, но это уже отдельная история.

5. Таким образом вертикальная опорная связь на опоре В, показанная ни рисунке 2.3, препятствует только вертикальному перемещению балки в точке В и соответствует скользящей шарнирной опоре, показанной на рисунке 2.1. Такая опора в точке В называется шарнирно подвижной опорой.

Казалось бы, для нашей линейки такое отображение опорных связей не подходит, никакой ярко выраженной горизонтальной связи у линейки по умолчанию нет (за исключением сил трения), но тут все зависит от того, какие именно задачи предстоит решать.

Достаточно часто балки рассчитываются на вертикальную нагрузку, действующую вдоль оси координат у, при этом никаких сил, действующих вдоль оси координат х, нет или их сумма равна 0. Кроме того, если приложенные горизонтальные нагрузки будут меньше, чем силы трения, возникающие на опорных участках балки под действием вертикальной нагрузки, то в таких случаях схема балки, приведенная на рисунке 2.3, для нашей линейки вполне допустима.

1.3 Жесткое защемление на опорах

Если пригрузить концы линейки еще книгами:

Рисунок 3.

то такую линейку можно условно рассматривать, как балку, защемленную на опорах, и тогда модель балки будет выглядеть так:

Рисунок 3.1

Физический смысл такого отображения опор следующий: жесткая заделка препятствует не только вертикальному и горизонтальному перемещению балки на опоре, но также и повороту. т.е. ограничивает все 3 степени свободы физического тела. Такая опора называется жестким защемлением или глухой заделкой.

Мы можем легко в этом убедиться, если уберем одну из стопок книг. Линейка, защемленная в другой стопке, останется на месте.

Опять же в данном случае рассматривать балку как жестко защемленную не совсем правильно, если опорные участки достаточно короткие, а вот если книги с линейкой хорошо проклеить, и опорные участки у линейки сравнительно длинные, то после высыхания клея линейку уже можно рассматривать как балку, жестко защемленную на опорах.

Но все равно чаще всего при расчетах принимается вариант опор, показанный на рисунке №2.3. А вот железобетонные балки, которые бетонируются одновременно со стенами или металлические балки, жестко приваренные или прикрученные к очень жесткому основанию так, что составляют как бы единое целое, можно рассматривать как балки, защемленные на концах.

1.4. Скользящие заделки

Рисунок 3.2. а) заделка, скользящая относительно оси х; б) заделка, скользящая относительно оси у.

Т.е. одна из склеенных стопок книг нами по-прежнему рассматривается как глухая заделка на опоре А, а вот заделки на опоре В уже рассматриваются как скользящие. Такие заделки называются скользящими заделками или жесткими заделками с одной степенью свободы перемещения.

1.5. Если продолжить мысль и представить, что наша линейка очень прочно склеена из отдельных кусочков, то получается, что мы можем рассматривать любой участок нашей линейки, например, между отметками 5 и 15 см, как отдельную балку со скользящей заделкой на концах и могли бы изобразить нашу балку не как одну балку на двух шарнирных опорах, а как 2, 3 и сколь угодно много балок, из которых крайние балки имели бы по одной шарнирной опоре и на втором конце скользящую заделку, а все остальные балки имели бы скользящую заделку. В данном случае в таком усложнении задачи нет никакой необходимости, но часто такое допущение позволяет решать достаточно сложные задачи.

А чтобы такое предположение было корректным, мы для упрощения решения задачи должны рассекать нашу балку очень аккуратно в плоскости, перпендикулярной оси х и таким образом мы получим сколь угодно большое количество поперечных сечений балки. Зачем нужно рассматривать поперечные сечения, мы узнаем чуть позже.

Все. Больше никаких вариантов опор при решении задач по расчету строительных конструкций не рассматривается: или шарнирные опоры или заделка (защемление) на концах. Другое дело, что шарнирных опор у балки может быть сколь угодно много, один конец может быть защемлен, опоры, как шарнирные таки и жесткие, могут быть скользящими, шарнирные опоры могут давать осадку и даже представлять собой сплошное упругое основание, у балки могут быть консоли, но это уже варианты не опор, а варианты расположения и комбинации опор. Таких комбинаций может быть бесконечно много, но это уже не основы теоретической механики и здесь мы эти варианты рассматривать не будем.

Ну а теперь выясним, зачем нужно было городить эту конструкцию и что она нам дает.

2. Нагрузки (наружные силы).

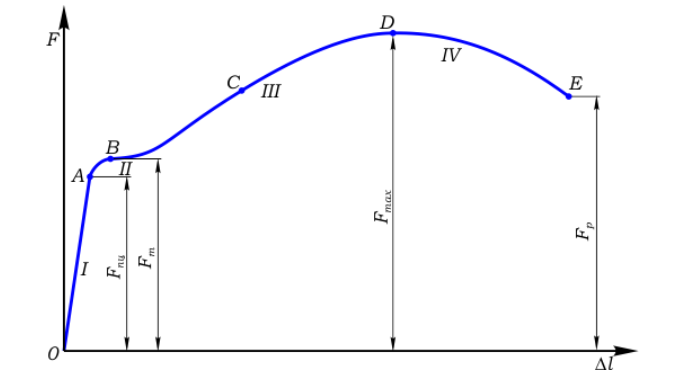
Если повнимательнее присмотреться к рисунку 1, то можно увидеть, что линейка немного прогнулась посредине. Если взять более длинную 40-сантиметровую линейку и опереть ее на книги, то прогиб посредине линейки будет еще более заметным, но все равно пока не очень явным.

Почему же это случилось?

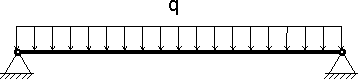
Рисунок 5.

2.1. Распределенная нагрузка может быть равномерной, как показано на рисунке 5, так и неравномерно распределенной, при этом значение распределенной нагрузки может изменяться линейно и не линейно, кроме того распределенная нагрузка может действовать не на всю длину балки, а на один или несколько участков. Если на балку действует несколько равномерно распределенных нагрузок, например: собственный вес, вес от кирпичной кладки, опирающейся на балку, и нагрузка от плит перекрытия то такие распределенные нагрузки можно суммировать, что в дальнейшем значительно облегчает расчеты. Подобный подход называется принципом суперпозиции.

2.2. Если у Вас есть палец, а я думаю, таковых у Вас имеется немало, то при надавливании пальцем на середину линейки линейка прогнется уже значительно заметнее. В этом случае на линейку действует кроме равномерно распределенной нагрузки еще и сосредоточенная (точечная) нагрузка (на рисунке 6 распределенная нагрузка не показана):

Рисунок 6.

Само собой точечных нагрузок может быть сколь угодно много и прикладываться они могут в любом месте балки и не только перпендикулярно оси балки, но и параллельно. Если сосредоточенная нагрузка приложена перпендикулярно на опоре, то на балку это никак не повлияет, просто возникнет реакция опоры численно равная нагрузке и направленная противоположно. Вы можете это легко проверить сами, надавив пальцем на линейку в месте опоры на одну из книг, если уж очень сильно давить, то Вы скорее промнете книгу, но линейка все равно не прогнется.

Почему так происходит?

Оказывается нагрузка, действуя на балку, создает изгибающий момент, т.е. хочет повернуть балку вокруг опор. При этом значение изгибающего момента напрямую зависит не только от величины нагрузки, но и от плеча действия силы. Нетрудно догадаться, что максимальный изгибающий возникает тогда, когда сосредоточенная нагрузка действует на балку посредине.

Конечно же действует этот момент на балку не просто так, а в рассматриваемом поперечном сечении балки и возникает он в данном случае от действия опорной реакции, которую еще следует определить, но об этом разговор пойдет дальше.

Иногда при расчетах вводится понятие вращающего момента, действующего на балку:

Рисунок 7.

Ну и теперь непосредственно сам сопромат, потому как до этого описывались термины и понятия теоретической механики.

3. Напряжения (внутренние силы).

Если на линейку, опертую на книги, как показано на рисунке 1, продолжать давить пальцем, то линейка будет прогибаться все сильнее и сильнее, пока в один прекрасный момент не поломается (конечно, вместо грубой физической силы Вы можете использовать мощь своего интеллекта, я возражать не буду)

Почему это происходит?

Оказывается всему есть предел и в данном случае был преодолен предел сопротивления материала (древесины), из которого изготовлена линейка.

Если к примеру взять стальную полосу с такими же параметрами сечения и такой же длины, как у деревянной линейки и тоже положим ее на книги и приложим к ней такую же нагрузку посередине, то поломать стальную полосу пальцем уже вряд ли получится, как минимум потому, что сопротивление стали в десятки раз больше сопротивления древесины. Но вернемся к рассмотрению деревянной линейки.

Когда Вы давите пальцем на линейку, то линейка деформируется, верхняя часть линейки сжимается и, соответственно в этой области возникают сжимающие нормальные напряжения. Нижняя часть линейки растягивается и, соответственно в этой области возникают растягивающие нормальные напряжения. Эти напряжения являются реакцией материала на действующую нагрузку.

Нормальными называются напряжения, направленные по нормали (перпендикулярно) рассматриваемому поперечному сечению балки.

Кроме нормальных в рассматриваемых сечениях могут возникать и касательные напряжения, а еще напряженные состояния могут быть не только линейными, но еще плоскими или объемными, но об этом опять же не сейчас.

Теория сопротивления материалов предполагает, что при таком действии нагрузки в середине поперечного сечения балки деформация равна 0 и, соответственно, никаких нормальных напряжений, ни растягивающих, ни сжимающих в середине поперечного сечения балки нет, а максимальные напряжения возникают посредине пролета балки сверху и снизу поперечного сечения. При этом эпюры внутренних нормальных напряжений в поперечных сечениях балки будут выглядеть так:

Рисунок 8.

Разрушение конструкции может начинаться как в верхней так и в нижней части. Расчет конструкции на прочность сводится к тому, чтобы этого самого разрушения не допустить. Другими словами, максимально возможные напряжения должны быть меньше сопротивления материала. В данном случае:

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Соизвольте принять Низкий поклон, флотский
Доктор Лом. Долгих лет Вашей мыслящей голове. Я очень небольшой изобретатель, очень нужен расчет конструкций и из дерева и из метала.

Мой сайт всегда к Вашим услугам, в разделе: «Расчет конструкций» есть примеры расчета некоторых наиболее распространенных деревянных и металлических конструкций. Там же можно задать более конкретный вопрос.

Док, спасибо огромное за то, что умеете доходчиво объяснить такие специфические науки как теор мех и сопромат. Я инженер-строитель и мне очень важно это знать. Начал разбираться 2 месяца назад, по вашим лекциям, с самого нуля (в институте дурака валял, а щас работа обязывает). Вопросов конечно много, но очень многое я смог понять, о чем раньше и представления не имел. Спасибо, док!

Большое спасибо автору.

Автору спасибо. Помнится в колледже мы расчитывали оч сложные вещи и называлось у нас это не сопромат, а прикладная механика. БУдем вспоминать

О,как я ненавидела сопромат. Но, в первый раз читая эту статью он мне стал интересен. Спасибо.

благодарен за информацию.горная академия заочно.

Насколько важен способ подачи материала. Просто, доходчиво, на пальцах. Лично я 30 лет назад это проходил, но хлопцы на форуме постоянно задают вопросы по основам. Так что линк забил. Спасибо.

Когда-то, в молодости, из-за сопромата бросила Бауманку.Сейчас приходиться наверстывать упущенное. Учусь заочно, дистанционно по строительной специальности. Думала никогда мне не понять этот предмет. Теперь, по-немногу, что-то проясняется. Огромное спасибо.

очень доступно и просто, спасибо!

Умно и просто изложено. «Отче наш» учите так же. )

Доктор Лом, спасибо за Ваши труды! Очень мне сейчас пригождаются в освежении знаний и ликвидации пробелов первых курсов ВУЗа.

Огромное спасибо!! Удачи автору!

Спасибо. Просто и понятно)))

Очень интересный ресурс с доходчивым изложением. Огромное спасибо автору за такой титанический труд.
Мне кажется что в тексте есть опечатки: во-первых, два пункта с номером 1.3, а во-вторых, в первом пункте 1.3 фразу «а опирается линейка, если очень хорошо присмотреться на выступающие корешки линейки» следует заменить на «а опирается линейка, если очень хорошо присмотреться на выступающие корешки книг»

Все верно (к сожалению времени на написание статей у меня критически мало, от того и случаются оплошности). Сейчас исправлю. Спасибо за внимательность.

Посмотрите статью «Виды опор, какую расчетную схему выбрать». Здесь же скажу, что если длина опорных участков плиты около половины толщины плиты, то это просто шарнирно опертая плита.

Соизвольте принять Низкий поклон, флотский
Доктор Лом. Долгих лет Вашей мыслящей голове. Я очень небольшой изобретатель, но очень нужен расчет каркаса вакуумного аэростата из углепластика. Аэростат нужен для получения экологически чистой электроэнергии в промышленных масштабах. Энергия ветра(скорость) на высоте от 500м намного больше, чем на высотах существующих ветряков. Аэростат(его величество Архимед) должен поднять конструкций длиной 1500-2000м. Выше плотность воздуха уменьшается и уменьшается сила Архимеда и уменьшается сила ветра. На вертикальном ветропарке, может работать моей конструкции 50-60ветродвигателей. Энергию ветра необходимо аккумулировать, так как скорость ветра не стабильна. Наилучший аккумулятор это энергия сжатого воздуха в замкнутом объеме. Поэтому ветродвигатели должны вращать винтовые компрессоры. Полученный сжатый воздух идет в низ, в ресиверы. На энергии сжатого воздуха в одну атмосферу работают на полную мощность мои двигатели и вращают типовой электрогенераторы. Уважаемый Доктор Лом, мы наверно одного возраста, значит осталось жить не долго. Давайте попробуем сделать что-то необычное. Что бы доказать, что не напрасно жили на божьем свете, не напрасно нас родили. Один я не вытяну, т.к. я весьма малограмотен.

спасибо автору, очень все понятно. Я, правда, еще в 10 классе, но иду на инженера и судя по всему это очень важный предмет, поэтому начну-ка изучать его сейчас

Доктор Лом, все статьи Вашего сайта написаны на высоком уровне! Спасибо и долгих счастливых Вам лет!

Здравствуйте. Меня интересуют некоторые вопросы по фундаменту для печи и фундаменту дома. Я хотел бы сделать перевод с карты Сбербанка на Вашу карту Сбербанка, т.к. яндекс кошелька у меня нет и других способов оплаты, кроме оплаты наличными я не знаю. Сообщите, пожалуйста, на какую карту сбербанка перевести деньги, или как ещё можно решить вопрос оплаты, не заводя яндекс-кошелька. Я опасаюсь заводить яндекс кошелёк, считая весьма вероятной возможность потерять деньги, в нём хранящиеся. Спасибо.

Юрий Николаевич, перевести деньги на яндекс-кошелек можно с любой карточки и даже с мобильного телефона, наличие собственного яндекс-кошелька совершенно не обязательно.

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник

Что такое сопромат